题目内容
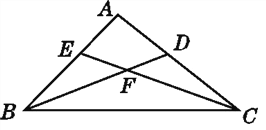
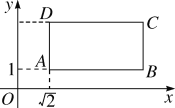
【题目】已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线y=﹣m(m> ![]() )于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
)于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
(1)求证:△ABC≌△AOD;
(2)设△ACD的面积为S,求S关于m的函数关系式;
(3)若四边形ABCD恰有一组对边平行,求m的值.
【答案】
(1)解:证明:∵A(0,5),B(3,1),
∴AB= ![]() =5,
=5,
∴AB=OA,
∵AB⊥BC,
∴∠ABC=90°,
在Rt△ABC和Rt△AOD中,
![]() ,
,
∴Rt△ABC≌Rt△AOD
(2)解:解:过点B作直线BE⊥直线y=﹣m于E,作AF⊥BE于F,如图,

∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
∴Rt△ABF∽Rt△BCE,
∴ ![]() ,即
,即 ![]() ,
,
∴BC= ![]() (m+1),
(m+1),
在Rt△ACB中,AC2=AB2+BC2=25+ ![]() (m+1)2,
(m+1)2,
∵△ABC≌△AOD,
∴∠BAC=∠OAD,即∠4+∠OAC=∠OAC+∠5,
∴∠4=∠5,
而AO=AB,AD=AC,
∴△AOB∽△ACD,
∴ ![]() =
= ![]() ,
,
而S△AOB= ![]() ×5×3=
×5×3= ![]() ,
,
∴S= ![]() (m+1)2+
(m+1)2+ ![]() (m>
(m> ![]() )
)
(3)解:作BH⊥y轴于H,如图,
当AB∥CD时,则∠ACD=∠CAB,
而△AOB∽△ACD,
∴∠ACD=∠AOB,
∴∠CAB=∠AOB,
而tan∠AOB= ![]() =3,tan∠ACB=
=3,tan∠ACB= ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =3,解得m=8;
=3,解得m=8;
当AD∥BC,则∠5=∠ACB,
而△AOB∽△ACD,
∴∠4=∠5,
∴∠ACB=∠4,
而tan∠4= ![]() ,tan∠ACB=
,tan∠ACB= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得m=3.
综上所述,m的值为3或8
【解析】(1)由A、B两点坐标根据勾股定理求出AB的值,根据HL得到Rt△ABC≌Rt△AOD;(2)根据题意得到Rt△ABF∽Rt△BCE,得到比例,求出BC的值,得到△AOB∽△ACD,根据相似三角形的面积之比等于相似比的平方,求出S关于m的函数关系式;(3)由△AOB∽△ACD,得到比例,再根据三角函数值求出m的值.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方,以及对锐角三角函数的定义的理解,了解锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】中考前的模拟考试对于学生来说具有重大的指导意义,现抽取m名学生的数学一模成绩进行整理分组,形成如下表格(x代表成绩,规定x>140为优秀),并绘制出扇形统计图和频数分布直方图(横坐标表示成绩,单位:分).
A组 | 140<x≤150 |
B组 | 130<x≤140 |
C组 | 120<x≤130 |
D组 | 110<x≤120 |
E组 | 100<x≤110 |
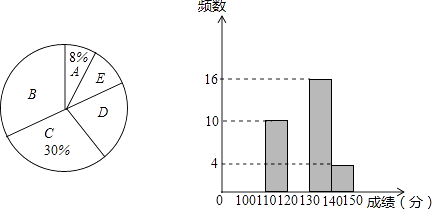
(1)m的值为;扇形统计图中D组对应的圆心角是°.
(2)若要从成绩优秀的学生甲、乙、丙、丁中,随机选出2人介绍经验,求甲、乙两人中至少有1人被选中的概率(通过画树状图或列表法进行分析).