题目内容
【题目】某商场同时购进甲、乙两种商品共![]() 件,其进价和售价如右表,设其中甲种商品购进
件,其进价和售价如右表,设其中甲种商品购进![]() 件.
件.
(1)直接写出购进乙种商品的件数;(用含![]() 的代数式表示)
的代数式表示)
(2)若设该商场售完这![]() 件商品的总利润为
件商品的总利润为![]() 元.
元.
①求![]() 与
与![]() 的函数关系式;
的函数关系式;
②该商品计划最多投入![]() 元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?
元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?
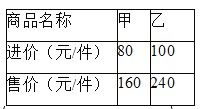
【答案】(1)购进乙种商品的件数是(200﹣x)件;(2)①y=﹣60x+28000(0≤x≤200);②该商场获得的最大利润为22000元.
【解析】分析:(1)同时购进甲、乙两种商品共![]() 件,甲种商品购进
件,甲种商品购进![]() 件, 购进乙种商品的件数是(200﹣x)件;
件, 购进乙种商品的件数是(200﹣x)件;
(2)①根据总利润=(甲的售价-甲的进价)×购进甲的数量+(乙的售价-乙的进价)×购进乙的数量代入列关系式,并化简;
②根据总成本≤18000列不等式即可求出x的取值,再根据函数的增减性确定其最值问题;
详解:(1)购进乙种商品的件数是![]() 件;
件;
(2) ①根据题意得:y=(16080)x+(240100)(200x),
=60x+28000,
则y与x的函数关系式为:y=60x+28000;
②![]()
解得:![]()
∴至少要购进100件甲商品,
y=60x+28000,
∵60<0,
∴y随x的增大而减小,
∴当x=100时,y有最大值,
y大=60×100+28000=22000,
∴若售完这些商品,则商场可获得的最大利润是22000元;

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目