题目内容
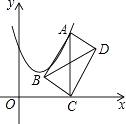
【题目】如图,在△ABC中,AB=2,AC=![]() ,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.
,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.

【答案】2
【解析】∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∵∠BAC=105°
∴∠DAE=135°.
∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
∴在△ABC与△DBF中,
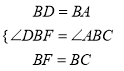 ,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=![]() ,
,
同理可证△ABC≌△EFC,
∴AB=EF=AD=2,
∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°-∠DAE=45°,
根据勾股定理可求得平行四边形DAEF边AD上的高为1,
∴平行四边形AEFD的面积是![]() .
.

练习册系列答案
相关题目