题目内容
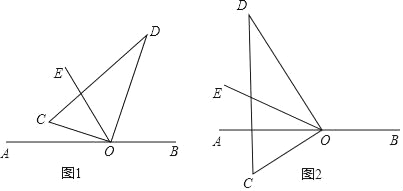
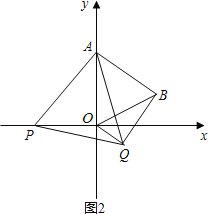
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
【答案】(1)B(![]() ,1);(2)∠ABQ=90°,始终不变.(3)P的坐标为(﹣
,1);(2)∠ABQ=90°,始终不变.(3)P的坐标为(﹣![]() ,0)
,0)
【解析】
试题分析:(1)如图,作辅助线;证明∠BOC=30°,OB=2,借助直角三角形的边角关系即可解决问题;
(2)证明△APO≌△AQB,得到∠ABQ=∠AOP=90°,即可解决问题;
(3)根据点P在x的正半轴还是负半轴两种情况讨论,再根据全等三角形的性质即可得出结果.
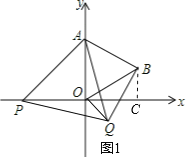
解:(1)如图1,过点B作BC⊥x轴于点C,
∵△AOB为等边三角形,且OA=2,
∴∠AOB=60°,OB=OA=2,
∴∠BOC=30°,而∠OCB=90°,
∴BC=![]() OB=1,OC=
OB=1,OC=![]() ,
,
∴点B的坐标为B(![]() ,1);
,1);
(2)∠ABQ=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ、AO=AB、∠PAQ=∠OAB,
∴∠PAO=∠QAB,
在△APO与△AQB中,
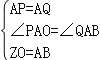 ,
,
∴△APO≌△AQB(SAS),
∴∠ABQ=∠AOP=90°;
(3)当点P在x轴负半轴上时,点Q在点B的下方,
∵AB∥OQ,∠BQO=90°,∠BOQ=∠ABO=60°.
又OB=OA=2,可求得BQ=![]() ,
,
由(2)可知,△APO≌△AQB,
∴OP=BQ=![]() ,
,
∴此时P的坐标为(﹣![]() ,0).
,0).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目