题目内容
【题目】问题提出:
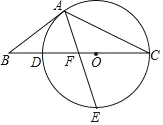
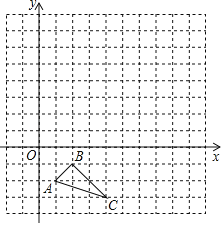
(1)如图1,在四边形ABCD中,AB=BC,AD=CD=3,∠BAD=∠BCD=90°,∠ADC=60°,则四边形ABCD的面积为 ;
问题探究:
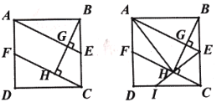
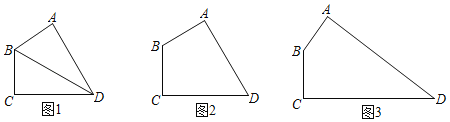
(2)如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=135°,AB=2![]() ,BC=3,在AD、CD上分别找一点E、F,使得△BEF的周长最小,并求出△BEF的最小周长;
,BC=3,在AD、CD上分别找一点E、F,使得△BEF的周长最小,并求出△BEF的最小周长;
问题解决:
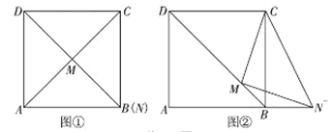
(3)如图3,在四边形ABCD中,AB=BC=2,CD=10,∠ABC=150°,∠BCD=90°,则在四边形ABCD中(包含其边沿)是否存在一点E,使得∠AEC=30°,且使四边形ABCE的面积最大.若存在,找出点E的位置,并求出四边形ABCE的最大面积;若不存在,请说明理由.
【答案】(1)3![]() ;(2)△BEF的最小周长为2
;(2)△BEF的最小周长为2![]() ;(3)8+4
;(3)8+4![]() ,见解析
,见解析
【解析】
(1)利用SAS可证明△ABD≌△CBD,可得∠ADB=∠CDB=30°,进而可求AB的长,进一步即可求出四边形ABCD的面积;
(2)如图,作点B关于AD的对称点M,作点B关于CD的对称点N,连接MN,交AD于点E,交CD于点F,由轴对称的性质可得△BEF的最小周长即为MN的长,再由勾股定理求出MN的长即得结果;
(3)作△ABC的外接圆,交CD于点E,连接AC,AE,过点A作AM⊥CD于点M,作BN⊥AM于点N,由圆内接四边形的性质可得∠AEC=30°,由矩形的性质和解直角三角形的知识可求得AM与CM的长,进一步即可求得AE与CE的长,进而确定当点E在AC的垂直平分线上时,S四边形ABCE最大,问题即得解决.
解:(1)∵AB=BC,AD=CD=3,∠BAD=∠BCD=90°,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵∠ADC=60°,
∴∠ADB=∠CDB=30°,
∴AB=BC=![]() ,
,
∴四边形ABCD的面积=2S△ABD=2×![]() ×3×
×3×![]() =3
=3![]() .
.
故答案为:3![]() ;
;
(2)如图,作点B关于AD的对称点M,作点B关于CD的对称点N,连接MN,交AD于点E,交CD于点F,过点M作MG⊥BC,交CB的延长线于点G,
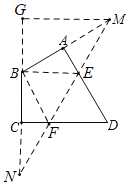
∵点B,点M关于AD对称,∴BE=EM,AB=AM=2![]() ,∴BM=4
,∴BM=4![]() ,
,
∵点B,点N关于CD对称,∴BF=FN,BC=CN=3,
∴△BEF的周长=BE+BF+EF=NF+EF+EM=MN,
由轴对称的性质知:此时MN的长即为△BEF周长的最小值.
∵∠ABC=135°,∴∠GBM=45°,
∴∠GBM=∠GMB=45°,
∴BG=GM,
∵BG2+GM2=BM2,
∴BG=4=GM,
∴GN=BG+BC+CN=4+3+3=10,
∴在Rt△GMN中,MN=![]() =
=![]() =2
=2![]() ,
,
∴△BEF的最小周长为2![]() .
.
(3)作△ABC的外接圆,交CD于点E,连接AC,AE,过点A作AM⊥CD于点M,作BN⊥AM于点N,
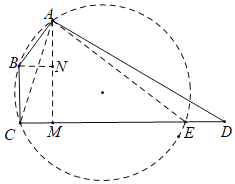
∵四边形ABCE是圆内接四边形,
∴∠ABC+∠AEC=180°,
∴∠AEC=30°,
∵BN⊥AM,AM⊥CD,∠BCD=90°,
∴四边形BCMN是矩形,
∴BC=MN=2,BN=CM,∠CBN=90°,
∵∠ABC=150°,
∴∠ABN=60°,∴∠BAN=30°,
∴BN=![]() AB=1,AN=
AB=1,AN=![]() BN=
BN=![]() ,
,
∴AM=![]() +2,CM=1,
+2,CM=1,
∵∠AEC=30°,AM⊥CE,
∴AE=2AM=2![]() +4,ME=
+4,ME=![]() AM=3+2
AM=3+2![]() ,
,
∴CE=CM+ME=4+2![]() =AE,
=AE,
∴点E在AC垂直平分线上,
∵S四边形ABCE=S△ABC+S△ACE,且S△ABC是定值,AC长度是定值,点E在△ABC的外接圆上,
∴当点E在AC的垂直平分线上时,S四边形ABCE最大,
此时S四边形ABCE=S四边形ABCM+S△AME=![]() ×
×![]() ×1+
×1+![]() =8+4
=8+4![]() .
.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 20 |
|
良好 | ||
合格 | 10 |
|
不合格 | 5 |
|
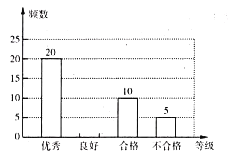
请根据以上信息,解答下列问题:
(1)本次调查随机抽取了______名学生;表中![]() ______,
______,![]() ______;
______;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.