题目内容
【题目】阅读第（1）题解答过程填理由，并解答第（2）题
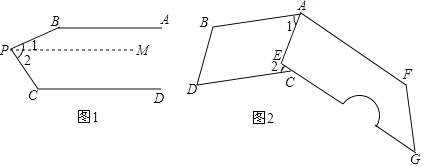
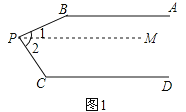
（1）已知：如图1，AB∥CD，P为AB，CD之间一点，求∠B+∠C+∠BPC的大小．
解：过点P作PM∥AB
∵AB∥CD（已知）
∴PM∥CD ，
∴∠B+∠1＝180°， ．
∴∠C+∠2＝180°
∵∠BPC＝∠1+∠2
∴∠B+∠C+∠BPC＝360°
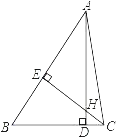
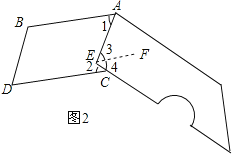
（2）我们生活中经常接触小刀，如图2小刀刀柄外形是一个直角梯形挖去一个小半圈，其中AF∥EG，∠AEG＝90°，刀片上、下是平行的（AB∥CD），转动刀片时会形成∠1和∠2，那么∠1+∠2的大小是否会随刀片的转动面改变，如不改变，求出其大小；如改变，请说明理由．
【答案】（1）如果两条直线都与第三条直线平行，那么这两条直线也互相平行；两直线平行，同旁内角互补；（2）不会变，∠1+∠2＝90°．
【解析】
（1）利用平行线的性质，根据两直线平行，同旁内角互补，即可求得答案；
（2）首先过点E作EF∥AB，根据两直线平行，内错角相等，即可求得答案．
解：（1）过点P作PM∥AB
∵AB∥CD（已知）
∴PM∥CD（如果两条直线都与第三条直线平行，那么这两条直线也互相平行），
∴∠B+∠1＝180°（两直线平行，同旁内角互补），
∴∠C+∠2＝180°（两直线平行，同旁内角互补），
∵∠BPC＝∠1+∠2，
∴∠B+∠C+∠BPC＝360°．
故答案为：如果两条直线都与第三条直线平行，那么这两条直线也互相平行；两直线平行，同旁内角互补．
（2）不会变，∠1+∠2＝90°．
理由：如图2，过点E作EF∥AB，
∵AB∥CD，
∴AB∥EF∥CD，
∴∠3＝∠1，∠4＝∠2，
∵∠AEC＝90°，即∠3+∠4＝90°，
∴∠1+∠2＝90°．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
