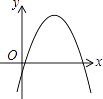题目内容
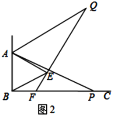
【题目】如图①所示是一个长为![]() ,宽为
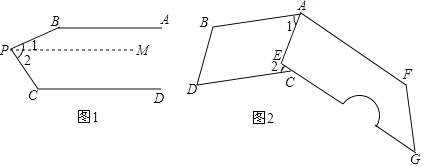
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
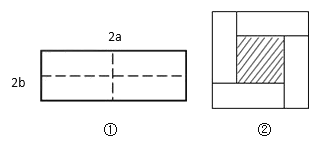
(1)图②中的阴影部分的正方形的边长等于 .(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积:
方法①: .
方法②: .
(3)观察图②,直接写出![]() 、
、![]() 、
、![]() 这三个代数式之间的等量关系.
这三个代数式之间的等量关系.
(4)根据(3)题中的等量关系,若![]() ,
,![]() ,求图②中阴影部分的面积.
,求图②中阴影部分的面积.
【答案】(1)a-b;(2) (ab)2, (a+b)24ab;(3)(ab)2=(a+b)24ab;(4)8
【解析】
(1)根据阴影部分可得边长(a-b);
(2) 方法①:直接读取阴影部分正方形的边长是a-b,再求面积;
方法②:用(a+b)为边长的正方形面积减去四个矩形面积即可;
(3)由上题的两个方法的出等量关系式即可;
(4)将a+b=12,ab=20的值代入上题中的等量关系式,再求阴影部分的面积即可.
解: (1)根据图形可得:阴影部分的正方形的边长a-b,
故答案为a-b;
(2)根据图形可得:
方法①:(ab)2
方法②:(a+b)24ab
故答案为:(ab)2,(a+b)24ab.
(3)由阴影部分的两个面积代数式相等,
∴(ab)2=(a+b)24ab;
(4)由题意得:(ab)2=(a+b)24ab
将![]() ,
,![]() 代入上式得:(ab)2=1444×20=64,
代入上式得:(ab)2=1444×20=64,
∵a-b>0,
∴a-b=8,
∴图②中阴影部分的面积为8.

【题目】某宾馆拥有客房90间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 200 | 240 | 270 | 300 |
y(间) | 90 | 70 | 55 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出)