题目内容
【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.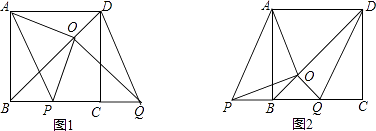
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB , BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.
【答案】
(1)解:四边形APQD为平行四边形;
(2)解:OA=OP,OA⊥OP,理由如下:
∵四边形ABCD是正方形,
∴AB=BC=PQ,∠ABO=∠OBQ=45°,
∵OQ⊥BD,
∴∠PQO=45°,
∴∠ABO=∠OBQ=∠PQO=45°,
∴OB=OQ,
在△AOB和△OPQ中,
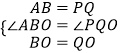
∴△AOB≌△POQ(SAS),
∴OA=OP,∠AOB=∠POQ,
∴∠AOP=∠BOQ=90°,
∴OA⊥OP;
(3)解:如图,过O作OE⊥BC于E.
①如图1,当P点在B点右侧时,
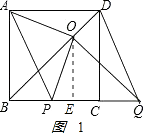
则BQ=x+2,OE= ![]() ,
,
∴y= ![]() ×
× ![]() x,即y=
x,即y= ![]() (x+1)2﹣
(x+1)2﹣ ![]() ,
,
又∵0≤x≤2,
∴当x=2时,y有最大值为2;
②如图2,当P点在B点左侧时,
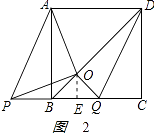
则BQ=2﹣x,OE= ![]() ,
,
∴y= ![]() ×
× ![]() x,即y=﹣
x,即y=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
又∵0≤x≤2,
∴当x=1时,y有最大值为 ![]() ;
;
综上所述,∴当x=2时,y有最大值为2;
【解析】(1)根据平移的性质,可得PQ∥AD且PQ=AD,然后根据一组对边平行且相等的四边形是平行四边形进行证明即可;
(2)先证明△BOQ为等腰直角三角形,从而可得到∠OQP=∠ABO,由平移的性质和正方形的性质可得到PQ=AB,然后依据SAS可证明△AOB≌△POQ,根据全等三角形的判定与性质,可得AO与OP的数量关系,根据余角的性质,可得AO与OP的位置关系;
(3)根据等腰直角三角形的性质,可得OE的长,根据三角形的面积公式可得到y与x的二次函数关系式,最后,根据二次函数的性质求解即可.

【题目】为了鼓励市民节约用水,万州市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费![]() 自来水销售费用
自来水销售费用![]() 污水处理费用)
污水处理费用)
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元 | 单价:元 |
17吨及以下 |
| 0.80 |
超过17吨不超过30吨的部分 |
| 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2013年3月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求![]() ,
,![]() 的值.
的值.
(2)随着夏天的到来,用水量将增加。为了节省开支,小梦计划把6月份的水费控制在不超过家庭月收入的2%,若小梦加的月收入为9200元,则小王家6月份最多能用水多少吨?