题目内容
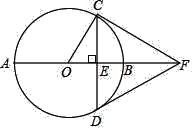
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,过点C的切线交AB的延长线于点F,连接DF.
(1)求证:DF是⊙O的切线;
(2)连接BC,若∠BCF=30°,BF=2,求CD的长.
【答案】(1)见解析;(2)2![]() .
.
【解析】
(1) 连接OD, 直径AB⊥弦CD,可得CE=ED,即OF为CD的垂直平分线,可得DF是⊙O的切线;
(2) 由∠BCF=30°,BF=2,可得△OCB为等边三角形,在Rt△OCE中可求得CE的长进而求得CD的长.
(1)证明:连接OD,如图,
∵CF是⊙O的切线
∴∠OCF=90°,
∴∠OCD+∠DCF=90°
∵直径AB⊥弦CD,
∴CE=ED,即OF为CD的垂直平分线
∴CF=DF,
∴∠CDF=∠DCF,
∵OC=OD,
∴∠CDO=∠OCD
∴∠CDO+∠CDB=∠OCD+∠DCF=90°,
∴OD⊥DF,
∴DF是⊙O的切线;
(2)解:∵∠OCF=90°,∠BCF=30°,
∴∠OCB=60°,
∵OC=OB,
∴△OCB为等边三角形,
∴∠COB=60°,
∴∠CFO=30°
∴FO=2OC=2OB,
∴FB=OB=OC=2,
在Rt△OCE中,∵∠COE=60°,
∴OE=![]() OC=1,
OC=1,
∴CE=![]() OE=
OE=![]() ,
,
∴CD=2CE=![]() .
.

练习册系列答案
相关题目