Question

【题目】已知：点C为∠AOB内一点．

（1）在OA上求作点D，在OB上求作点E，使△CDE的周长最小，请画出图形；（不写做法，保留作图痕迹）

（2）在（1）的条件下，若∠AOB＝30°，OC＝10，求△CDE周长的最小值．

Answer 1

【答案】（1）见解析；（2）△CDE周长的最小值为10．

【解析】

（1）分别作C点关于OA、OB的对称点M、N，然后连接MN分别交OA、OB于D、E，利用两点之间线段最短可判断此时△CDE的周长最小；

（2）利用对称的性质得到OM=OC=10，∠MOA=∠COA，ON=OC=10，∠NOB=∠COB，则△DCE的周长为MN，再证明△OMN为等边三角形，从而得到MN=OM=10，所以△CDE周长的最小值为10．

（1）如图，△CDE为所作；

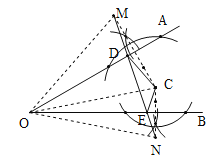
（2）∵点M与点C关于OA对称，

∴OM=OC=10，∠MOA=∠COA，DM=DC．

∵点N与点C关于OB对称，

∴ON=OC=10，∠NOB=∠COB，EC=EN，

∴△DCE的周长为CD+CE+DE=DM+DE+EN=MN，

∴此时△DCE的周长最小．

∵∠MOA+∠NOB=∠COA+∠COB=∠AOB=30°，

∴∠MON=30°+30°=60°，

∴△OMN为等边三角形，

∴MN=OM=10，

∴△CDE周长的最小值为10．