题目内容
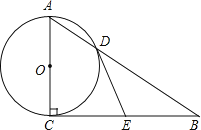
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2![]() ,则DB= ;
,则DB= ;
②当∠B= 度时,以O,D,E,C为顶点的四边形是正方形.
【答案】(1)详见解析;(2)①3![]() ;②45.
;②45.
【解析】
(1)证出EC为⊙O的切线;由切线长定理得出EC=ED,再求得EB=ED,即可得出结论;
(2)①由含30°角的直角三角形的性质得出AB,由勾股定理求出BC,再根据BD=BCcos30°计算即可;
②由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°,然后根据有一组邻边相等的矩形是正方形,即可得到结论.
(1)证明:连接DO.
∵∠ACB=90°,AC为直径,
∴EC为⊙O的切线;
又∵ED也为⊙O的切线,
∴EC=ED,
又∵∠EDO=90°,
∴∠BDE+∠ADO=90°,
∴∠BDE+∠A=90°
又∵∠B+∠A=90°,
∴∠BDE=∠B,
∴BE=ED,
∴BE=EC;
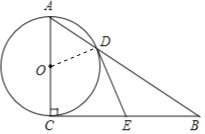
(2)解:①∵∠ACB=90°,∠B=30°,AC=2![]() ,
,
∴AB=2AC=4![]() ,
,
∴BC=![]() ,
,
∵AC为直径,
∴∠BDC=∠ADC=90°,
∴BD=BCcos30°=3![]()
故答案为:3![]() ;
;
②当∠B=45°时,四边形ODEC是正方形,
理由如下:
∵∠ACB=90°,
∴∠A=45°,
∵OA=OD,
∴∠ADO=45°,
∴∠AOD=90°,
∴∠DOC=90°,
∵∠ODE=90°,
∴四边形DECO是矩形,
∵OD=OC,
∴矩形DECO是正方形.
故答案为:45.

【题目】某校门口竖着“前方学校,减速慢行”的交通指示牌CD,数学“综合与实践”小组的同学将“测量交通指示牌CD的高度”作为一项课题活动,他们定好了如下测量方案:
项目 | 内容 |
课题 | 测量交通指示牌CD的高度 |
测量示意图 |
|
测量步骤 | (1)从交通指示牌下的点M处出发向前走10 米到达A处; (2)在点A处用量角仪测得∠DAM=27°; (3)从点A沿直线MA向前走10米到达B处;(4)在点B处用量角仪测得∠CBA=18°. |
请你帮助该小组同学根据上表中的测量数据,求出交通指示牌CD的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)