ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЉЕФЭМЯѓгы
ЃЉЕФЭМЯѓгы![]() жсНЛгк
жсНЛгк![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЎСЌНс
ЃЎСЌНс![]() СНЕуЕФзјБъЗжБ№ЮЊ
СНЕуЕФзјБъЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌЧвЕБ
ЃЌЧвЕБ![]() КЭ
КЭ![]() ЪБЖўДЮКЏЪ§ЕФКЏЪ§жЕ
ЪБЖўДЮКЏЪ§ЕФКЏЪ§жЕ![]() ЯрЕШЃЎ
ЯрЕШЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШєЕу![]() ЭЌЪБДг
ЭЌЪБДг![]() ЕуГіЗЂЃЌОљвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЗжБ№би
ЕуГіЗЂЃЌОљвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЗжБ№би![]() БпдЫЖЏЃЌЦфжавЛИіЕуЕНДяжеЕуЪБЃЌСэвЛЕувВЫцжЎЭЃжЙдЫЖЏЃЎЕБдЫЖЏЪБМфЮЊ
БпдЫЖЏЃЌЦфжавЛИіЕуЕНДяжеЕуЪБЃЌСэвЛЕувВЫцжЎЭЃжЙдЫЖЏЃЎЕБдЫЖЏЪБМфЮЊ![]() УыЪБЃЌСЌНс
УыЪБЃЌСЌНс![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() ЗелЃЌ
ЗелЃЌ![]() ЕуЧЁКУТфдк
ЕуЧЁКУТфдк![]() БпЩЯЕФ
БпЩЯЕФ![]() ДІЃЌЧѓ
ДІЃЌЧѓ![]() ЕФжЕМАЕу
ЕФжЕМАЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЖўДЮКЏЪ§ЭМЯѓЕФЖдГЦжсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУвд
ЃЌЪЙЕУвд![]() ЮЊЯюЕуЕФШ§НЧаЮгы
ЮЊЯюЕуЕФШ§НЧаЮгы![]() ЯрЫЦЃПШчЙћДцдкЃЌЧыЧѓГіЕу
ЯрЫЦЃПШчЙћДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉt=
ЃЛЃЈ2ЃЉt=![]() ЃЌ
ЃЌ 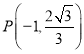 ЃЛЃЈ3ЃЉQЃЈ-1ЃЌ
ЃЛЃЈ3ЃЉQЃЈ-1ЃЌ![]() ЃЉЃЌМћНтЮі.
ЃЉЃЌМћНтЮі.
ЁОНтЮіЁП
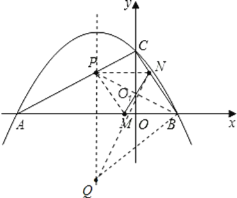
ЃЈ1ЃЉгЩЬтвтКЭЭМаЮПЩЧѓГіКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉНсКЯХзЮяЯпФкВПМИКЮЙиЯЕКЭаджЪЧѓГіtжЕМАPЕузјБъЃЛ
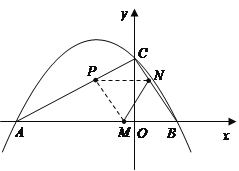
ЃЈ3ЃЉМйЩшГЩСЂЃЈ1ЃЉШєгаЁїACBЁзЁїQNBдђгаЁЯABC=ЁЯQBNЃЌбАевЯрЫЦЬѕМўЃЌХаЖЯЪЧЗёТњзуЃЎ
НтЃКЃЈ1ЃЉЁп![]() дкХзЮяЯпЩЯ
дкХзЮяЯпЩЯ
ЁрДњШыЕУc=![]()
Ёпx=-4КЭx=2ЪБЖўДЮКЏЪ§ЕФКЏЪ§жЕyЯрЕШЃЌ
ЁрЖЅЕуКсзјБъ![]() ,
,
![]() ,
,
гжЁпAЃЈ-3ЃЌ0ЃЉдкХзЮяЯпЩЯЃЌ
Ёр9a3b+![]() =0
=0
гЩвдЩЯЖўЪНЕУ![]() ;
;
ЃЈ2ЃЉгЩЃЈ1ЃЉ![]() ,
,
ЁрBЃЈ1ЃЌ0ЃЉЃЌ
СЌНгBPНЛMNгкЕуO1ЃЌИљОнелЕўЕФаджЪПЩЕУЃКO1вВЮЊPBжаЕуЃЎ
ЩшtУыКѓга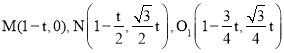 ,
,
ЩшPЃЈxЃЌyЃЉЃЌBЃЈ1ЃЌ0ЃЉ
ЁпO1ЮЊPЁЂBЕФжаЕуПЩЕУ![]() ЃЌМД
ЃЌМД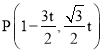 ,
,
ЁпAЃЌCЕузјБъжЊACЃК![]() ЃЌPЕувВдкжБЯпACЩЯДњШыЕУt=
ЃЌPЕувВдкжБЯпACЩЯДњШыЕУt=![]() ,
,
МД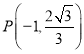 ЃЛ
ЃЛ
ЃЈ3ЃЉМйЩшГЩСЂЃЛ
ЂйШєгаЁїACBЁзЁїQNBЃЌдђгаЁЯABC=ЁЯQBNЃЌ
ЁрQЕудкxжсЩЯЃЌACЁЮQNЕЋгЩЬтжаAЃЌCЃЌQЃЌNзјБъжЊжБЯпЕФвЛДЮЯюЯЕЪ§ЮЊЃК![]() ЃЌ
ЃЌ
дђЁїACBВЛгыЁїQNBЯрЫЦЃЎ
ЂкШєгаЁїACBЁзЁїQBNЃЌдђга![]()
Щш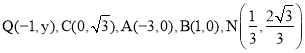 ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
ДњШыЃЈ1ЃЉЕУ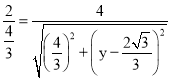 ЃЌ
ЃЌ
![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБгаQЃЈ-1ЃЌ
ЪБгаQЃЈ-1ЃЌ![]() ЃЉдђ
ЃЉдђ![]() ВЛТњзуЯрЫЦЩсШЅЃЛ
ВЛТњзуЯрЫЦЩсШЅЃЛ
ЕБy=![]() гаQЃЈ-1ЃЌ
гаQЃЈ-1ЃЌ![]() ЃЉдђ
ЃЉдђ![]() ЃЌ
ЃЌ
ЁрДцдкЕуQЃЈ-1ЃЌ![]() ЃЉЪЙЁїACBЁзЁїQBNЃЎ
ЃЉЪЙЁїACBЁзЁїQBNЃЎ
злЩЯПЩЕУЃКQЃЈ-1ЃЌ![]() ЃЉ.
ЃЉ.