题目内容
【题目】甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象，则下列叙述正确的个数为（ ）
（1）乙车的速度为80km/h（千米/小时）；（2）a=40，m=1；（3）甲车共行驶了7h；（4）乙车一定行驶了
h或
h，两车恰好距离50km．
A.1个B.2个C.3个D.4个
【答案】B
【解析】
（1）根据函数图象可得乙车行驶3.5-2=1小时与甲车相遇解答；（2）根据乙的速度，求出a的值和m的值解答；（3）再求出甲车行驶的路程y与时间x之间的解析式解答；（4）由解析式之间的关系建立方程解答．
（1）120÷（3.5-2）=80km/h（千米/小时），故正确；
（2）由题意，得
m=1.5-0.5=1．
120÷（3.5-0.5）=40（km/h），
则a=40．故正确
（3）当1.5＜x≤7时，甲车y与x之间的函数关系式为y=40x-20，
当y=260时，260=40x-20，
解得：x=7，
∴甲车共行驶时间是7-0.5=6.5小时，故错误
（4）当0≤x≤1时，设甲车y与x之间的函数关系式为y=k1x，由题意，得：
40=k1，
则y=40x
当1＜x≤1.5时，
y=40；
当1.5＜x≤7时，
设甲车y与x之间的函数关系式为y=k2x+b，由题意，得：
，
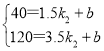解得：k2=40，b=-20，
则y=40x-20．
设乙车行驶的路程y与时间x之间的解析式为y=k3x+b3，由题意得：
，
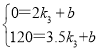解得：k3=80，b=-160，
则y=80x-160．
当40x-20-50=80x-160时，
解得：x=
．
当40x-20+50=80x-160时，
解得：x=
．
-2=
，-2=
．
所以乙车行驶小时或小时，两车恰好相距50km，故错误．
故选B．
