Question

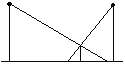
【题目】如图,一楼房AB后有一假山,其坡度为i=1∶,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高度.(注:坡度i是指坡面的铅直高度与水平宽度的比)

Answer 1

【答案】楼房AB的高度为(35+10)米.

【解析】试题分析：过点E作EF⊥BC于点F．在Rt△CEF中，求出CF= EF，过点E作EH⊥AB于点H．在Rt△AHE中，∠HAE=45°，得到CF的值，再根据AB=AH+BH，求出AB的值．

试题解析：过点E作EF⊥BC的延长线于F，EH⊥AB于点H，

在Rt△CEF中，

∵i==tan∠ECF，

∴∠ECF=30°，

∴EF=CE=10米，CF=10 米，

∴BH=EF=10米，HE=BF=BC+CF=（25+10）米，

在Rt△AHE中，∵∠HAE=45°，

∴AH=HE=（25+10）米，

∴AB=AH+HB=（35+10）米．

答：楼房AB的高为（35+10）米．