题目内容
【题目】在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=![]() ,连接PB,试探究PA、PB、PC满足的等量关系.
,连接PB,试探究PA、PB、PC满足的等量关系.
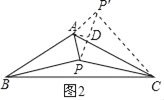
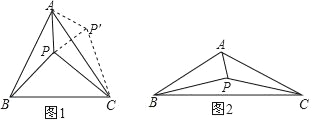
(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,连接PP′,如图1所示.由△ABP≌△ACP′可以证得△APP′是等边三角形,再由∠PAC+∠PCA=30°可得∠APC的大小为 度,进而得到△CPP′是直角三角形,这样可以得到PA、PB、PC满足的等量关系为 ;
(2)如图2,当α=120°时,参考(1)中的方法,探究PA、PB、PC满足的等量关系,并给出证明;
(3)PA、PB、PC满足的等量关系为 .
【答案】(1)150,PA2+PC2=PB2;(2)3PA2+PC2=PB2;(3)4PA2sin2![]() +PC2=PB2
+PC2=PB2
【解析】试题分析:(1)根据旋转变换的性质得到△PAP′为等边三角形,得到∠P′PC=90°,根据勾股定理解答即可;
(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,作AD⊥PP′于D,根据余弦的定义得到PP′=![]() PA,根据勾股定理解答即可;
PA,根据勾股定理解答即可;
(3)与(2)类似,根据旋转变换的性质、勾股定理和余弦、正弦的关系计算即可.
试题解析:
(1)∵△ABP≌△ACP′,
∴AP=AP′,
由旋转变换的性质可知,∠PAP′=60°,P′C=PB,
∴△PAP′为等边三角形,
∴∠APP′=60°,
∵∠PAC+∠PCA=![]() =30°,
=30°,
∴∠APC=150°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∴PA2+PC2=PB2,
故答案为:150,PA2+PC2=PB2;
(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=120°,P′C=PB,
∴∠APP′=30°,
∵∵∠PAC+∠PCA=![]() =60°,
=60°,
∴∠APC=120°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=30°,
∴PD=![]() PA,
PA,
∴PP′=![]() PA,
PA,
∴3PA2+PC2=PB2;
(3)如图2,与(2)的方法类似,
作将△ABP绕点A逆时针旋转α得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=α,P′C=PB,
∴∠APP′=90°﹣![]() ,
,
∵∵∠PAC+∠PCA=![]() ,
,
∴∠APC=180°﹣![]() ,
,
∴∠P′PC=(180°﹣![]() )﹣(90°﹣
)﹣(90°﹣![]() )=90°,
)=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=90°﹣![]() ,
,
∴PD=PAcos(90°﹣![]() )=PAsin
)=PAsin![]() ,
,
∴PP′=2PAsin![]() ,
,
∴4PA2sin2![]() +PC2=PB2,
+PC2=PB2,
故答案为:4PA2sin2![]() +PC2=PBspan>2.
+PC2=PBspan>2.