Question

【题目】如图，在平面直角坐标系中，已知点、，连接.如果点在直线上，且点到直线的距离不大于1，那么称点是线段的“临近点”.

（1）判断点是否是线段的“临近点”，并说明理由；

（2）若点是线段的“临近点”.①求的取值范围；②设直线与轴交于点，试用表达的面积，并求出的最大面积.

Answer 1

【答案】（1）是，见解析；（2）①3≤m≤5；②S=m-1；最大面积为4

【解析】

（1）把C代入y=x-1中检验，求出C到直线AB的距离，即可作出判断；

（2）①根据题意列出关于m的不等式，求出解集即可确定出m的范围；

②过A作AP⊥x轴于点P，交直线CQ于点M，过点Q作QN⊥AP于点N，求出M、N、P的坐标，利用S=表示出△ACQ的面积，再根据m的取值范围得出S的最大值.

解：（1）把x=代入y=x-1得：y=-1=，即C在直线y=x-1上，
∵C到线段AB的距离d=3-=＜1，

∴点是线段AB的“邻近点”；

（2）①若点Q（m，n）是线段AB的“邻近点”，则有n=m-1，且|n-3|≤1，
∴|m-4|≤1，即-1≤m-4≤1，
解得：3≤m≤5；

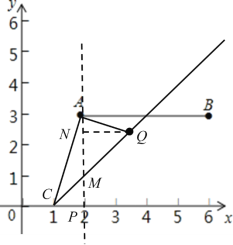
②如图，过A作AP⊥x轴于点P，交直线CQ于点M，过点Q作QN⊥AP于点N，

∵A（2，3），

在中，令y=0，则x=1，令x=2，则y=1，

∴点C（1，0），M（2，1），

∴S===m-1，

∵3≤m≤5，

∴S的最大值为5-1=4.