ЬтФПФкШн
ЁОЬтФПЁПдФЖСЯТСавЛЖЮЮФзжЃКвбжЊдкЦНУцФкСНЕуP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЁЂy2ЃЉЃЌЦфСНЕуМфЕФОрРыP1P2=![]()
ЮЪЬтНтОіЃКвбжЊAЃЈ1ЃЌ4ЃЉЁЂBЃЈ7ЃЌ2ЃЉ
ЃЈ1ЃЉЪдЧѓAЁЂBСНЕуЕФОрРыЃЛ
ЃЈ2ЃЉдкxжсЩЯеввЛЕуPЃЈВЛЧѓзјБъЃЌЛГіЭМаЮМДПЩЃЉЃЌЪЙPA+PBЕФГЄЖШзюЖЬЃЌЧѓГіPA+PBЕФзюЖЬГЄЖШЃЛ
ЃЈ3ЃЉдкxжсЩЯгавЛЕуMЃЌдкYжсЩЯгавЛЕуNЃЌСЌНгAЁЂNЁЂMЁЂBЕУЫФБпаЮANMBЃЌШєЫФБпаЮANMBЕФжмГЄзюЖЬЃЌЧыевЕНЕуMЁЂNЃЈВЛЧѓзјБъЃЌЛГіЭМаЮМДПЩЃЉЃЌЧѓГіЫФБпаЮANMBЕФзюаЁжмГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2![]() ЃЛЃЈ2ЃЉ6
ЃЛЃЈ2ЃЉ6![]() ЃЛЃЈ3ЃЉ10+2
ЃЛЃЈ3ЃЉ10+2![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнСНЕуМфЕФОрРыЙЋЪНПЩвдНтД№БОЬтЃЛ
ЃЈ2ЃЉИљОнСНЕужЎМфЯпЖЮзюЖЬКЭЕуЕФЖдГЦПЩвдНтД№БОЬтЃЛ
ЃЈ3ЃЉИљОнСНЕужЎМфЯпЖЮзюЖЬКЭЕуЕФЖдГЦПЩвдНтД№БОЬтЃЎ
НтЃКЃЈ1ЃЉЁпAЃЈ1ЃЌ4ЃЉЁЂBЃЈ7ЃЌ2ЃЉЃЌ
ЁрAB=![]()
=![]()
=2![]() ЃЌ
ЃЌ
МДAЁЂBСНЕуЕФОрРыЮЊЃК2![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчгвЭМ1ЫљЪОЃЌ
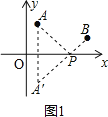
зїЕуAЙигкxжсЕФЖдГЦЕуAЁфЃЌ
ЁпAЃЈ1ЃЌ4ЃЉЁЂBЃЈ7ЃЌ2ЃЉЃЌ
ЁрAЁфЃЈ1ЃЌЉ4ЃЉЃЌ
ЁрAЁфB=![]() =6
=6![]() ЃЌ
ЃЌ
МДPA+PBЕФзюЖЬГЄЖШЪЧ6![]() ЃЛ
ЃЛ
ЃЈ3ЃЉзїЕуAЙигкyжсЕФЖдГЦЕуAЁфЃЌзїЕуBЙигкxжсЕФЖдГЦЕуBЁфЃЌСЌНгAЁфBЁфгкyжсНЛгкЕуNЃЌгыxжсНЛгкЕуMЃЌШчЭМ2ЫљЪОЃЌ

ЁпAЃЈ1ЃЌ4ЃЉЁЂBЃЈ7ЃЌ2ЃЉЃЌ
ЁрAЁфЃЈЉ1ЃЌ4ЃЉЃЌBЁфЃЈ7ЃЌЉ2ЃЉЃЌ
ЁрAB=![]() =2
=2![]() ЃЌ
ЃЌ
AЁфBЁф=![]() =10ЃЌ
=10ЃЌ
ЁрЫФБпаЮANMBЕФзюаЁжмГЄЪЧ10+2![]() ЃЎ
ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ