题目内容
【题目】函数y=kx+b和函数y=ax+m的图象如图所示,求下列不等式(组)的解集
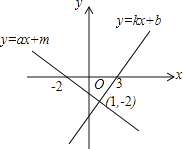
(1)kx+b<ax+m的解集是 ;
(2)![]() 的解集是 ;
的解集是 ;
(3)![]() 的解集是 ;
的解集是 ;
(4)![]() 的解集是 .
的解集是 .
【答案】(1)x<1.(2)x<﹣2(3)x>3.(4)﹣2<x<3.
【解析】
试题分析:(1)观察函数图象,结合交点的坐标以及函数图象的上下关系即可得出结论;
(2)观察函数图象,找出函数图象与x轴交点的坐标,结合图象在x轴上下的位置关系即可得出结论;
(3)观察函数图象,找出函数图象与x轴交点的坐标,结合图象在x轴上下的位置关系即可得出结论;
(4)观察函数图象,找出函数图象与x轴交点的坐标,结合图象在x轴上下的位置关系即可得出结论.
解:(1)观察函数图象,发现:
当x<1时,函数y=ax+b的图象在函数y=kx+b的图象的下方,
∴kx+b<ax+m的解集是:x<1.
故答案为:x<1.
(2)观察函数图象,发现:
当x<3时,函数y=kx+b的图象在x轴的下方;
当x<﹣2时,函数y=ax+b的图象在x轴的上方.
∴![]() 的解集为:x<﹣2.
的解集为:x<﹣2.
故答案为:x<﹣2.
(3)观察函数图象,发现:
当x>3时,函数y=kx+b的图象在x轴的上方;
当x>﹣2时,函数y=ax+b的图象在x轴的下方.
∴![]() 的解集为:x>3.
的解集为:x>3.
故答案为:x>3.
(4)观察函数图象,发现:
当x<3时,函数y=kx+b的图象在x轴的下方;
当x>﹣2时,函数y=ax+b的图象在x轴的下方.
∴![]() 的解集为:﹣2<x<3.
的解集为:﹣2<x<3.
故答案为:﹣2<x<3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目