题目内容
【题目】如图1,Rt△ACB 中,∠C=90°,点D在AC上,∠CBD=∠A,过A、D两点的圆的圆心O在AB上.
(1)利用直尺和圆规在图1中画出⊙O(不写作法,保留作图痕迹,并用黑色水笔把线条描清楚);
(2)判断BD所在直线与(1)中所作的⊙O的位置关系,并证明你的结论;
(3)设⊙O交AB于点E,连接DE,过点E作EF⊥BC,F为垂足,若点D是线段AC的黄金分割点(即 ![]() =
= ![]() ),如图2,试说明四边形DEFC是正方形).
),如图2,试说明四边形DEFC是正方形).
【答案】
(1)解:如图1,⊙O为所作;
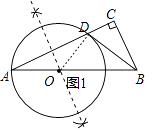
(2)解:BD与⊙O相切.理由如下:
连接OD,如图1,
∵OA=OD,
∴∠A=∠ODA,
∵∠CBD=∠A,
∴∠CBD=∠ODA,
∵∠C=90°,
∴∠CBD+∠CDB=90°,
∴∠ODA+∠CDB=90°,
∴∠ODB=90°,
∴OD⊥BD,
∴BD为⊙O的切线;
(3)解:∵∠CBD=∠A,∠DCB=∠BCA,
∴△CDB∽△CBA,
∴CD:CB=CB:CA,
∴CB2=CDCA,
∵点D是线段AC的黄金分割点, 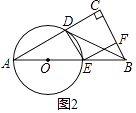
∴AD2=CDAC,
∵AD=CB,
∵AE为直径,
∴∠ADE=90°,
在△ADE和△BCD中
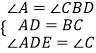 ,
,
∴△ADE≌△BCD,
∴DE=DC,
∵EF⊥BC,
∴∠EFC=90°,
∴四边形CDEF为矩形,
∴四边形DEFC是正方形.
【解析】(1)过A、D的圆圆心在AD的垂直平分线上,由交轨法,必在此线与AB的交点处;(2)要证相切,须连结半径,再证∠ODB=90°,可利用已知的∠C=90°,∠CBD=∠A即可证出;(3)由(2)中的△CDB∽△CBA可得CB2=CDCA,由已知“点D是线段AC的黄金分割点”可得AD2=CDAC,两式比较可得AD=CB,进而证得全等,所以DE=DC,易证四边形CDEF为矩形,即可证得四边形DEFC是正方形.

【题目】某校为了解九年级学生的身体素质情况,随机对九年级的50名学生进行一分钟跳绳次数测验,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | a |
第3组 | 120≤x<140 | 12 |
第4组 | 140≤x<160 | a+10 |
第5组 | 160≤x<180 |
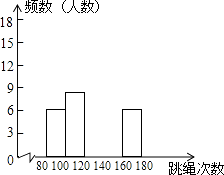
请结合图表完成以下问题.
(1)求出表中的a;
(2)补全频数分布直方图;
(3)若x≥140为优良,该校九年级有450名学生,请估计跳绳成绩达到优良的学生约有多少人?