题目内容
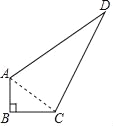
【题目】某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m.若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
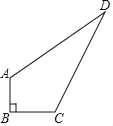
【答案】学校需要投入7200元买草皮.
【解析】
直接利用勾股定理的逆定理得出∠ACD=90°,再利用直角三角形的性质得出答案.
连接AC
∵∠B=90°,AB=3m,BC=4m,BC=12m,
AC2=AB2+AD2=32+42=25,AC=5m,
∴AC2+CD2=25+144=169=132
又∵AD2=132,
∴AC2+CD2=CD2
∴∠ACD=90°,
∴△ACD是直角三角形,
∴四边形ABCD的面积=6+30=36(m2),
∴学校要投入资金为:200×36=7200(元);
答:学校需要投入7200元买草皮.

练习册系列答案
相关题目
【题目】某校为了解九年级学生的身体素质情况,随机对九年级的50名学生进行一分钟跳绳次数测验,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | a |
第3组 | 120≤x<140 | 12 |
第4组 | 140≤x<160 | a+10 |
第5组 | 160≤x<180 |
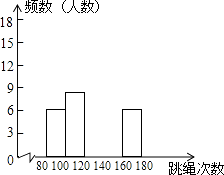
请结合图表完成以下问题.
(1)求出表中的a;
(2)补全频数分布直方图;
(3)若x≥140为优良,该校九年级有450名学生,请估计跳绳成绩达到优良的学生约有多少人?