题目内容
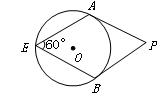
如图10,A、B、C、D、E、F是⊙O的六等分点.

(1) 连结AB、AD、AF,求证:AB+AF=AD;
(2) 若P是圆周上异于已知六等分点的动点,连结PB、PD、PF,试写出这三条线段的数量关系(不必说明理由).

(1) 连结AB、AD、AF,求证:AB+AF=AD;
(2) 若P是圆周上异于已知六等分点的动点,连结PB、PD、PF,试写出这三条线段的数量关系(不必说明理由).
(1)证明见解析(2) 当P在弧BF上时,PB+PF = PD;当P在弧BD上时,PB+PD= PF;
当P在弧DF上时,PD+PF=PB.
当P在弧DF上时,PD+PF=PB.
(1) 连结OB、OF.
∵A、B、C、D、E、F是⊙O的六等分点
∴ AD是⊙O的直径
且∠AOB=∠AOF=60°
∴ △AOB、△AOF是等边三角形
∴AB=AF=AO
∴AB+AF="AD···································" 5分
(2)当P在弧BF上时,PB+PF = PD;当P在弧BD上时,PB+PD= PF;
当P在弧DF上时,PD+PF=PB.
(1)连接OB、OF,得到等边△AOB、△AOF,据此并结合演的性质,即可推理出AB=AF=AO=OD,从而得到AB+AF=AD;
(2)分点P在不同的位置---在弧BF 上、在 弧BD 上、在 弧DF 上三种情况讨论.
∵A、B、C、D、E、F是⊙O的六等分点
∴ AD是⊙O的直径
且∠AOB=∠AOF=60°
∴ △AOB、△AOF是等边三角形
∴AB=AF=AO
∴AB+AF="AD···································" 5分
(2)当P在弧BF上时,PB+PF = PD;当P在弧BD上时,PB+PD= PF;
当P在弧DF上时,PD+PF=PB.
(1)连接OB、OF,得到等边△AOB、△AOF,据此并结合演的性质,即可推理出AB=AF=AO=OD,从而得到AB+AF=AD;
(2)分点P在不同的位置---在弧BF 上、在 弧BD 上、在 弧DF 上三种情况讨论.

练习册系列答案
相关题目
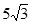 B
B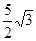 C8 D
C8 D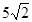
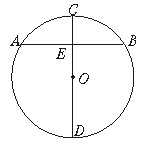
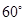 的圆心角所对的弦长为 .
的圆心角所对的弦长为 .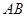 是⊙
是⊙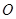 的直径,弦
的直径,弦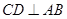 ,垂足为
,垂足为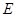 ,如果
,如果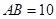 ,
,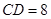 ,那么线段
,那么线段 的长是 .
的长是 .