��Ŀ����
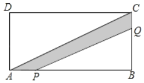
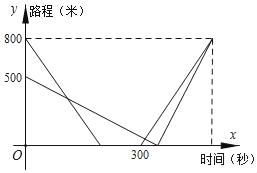
����Ŀ��ţţ�ͷ����ͬһֱ���ܵ�AB�Ͻ��������ܣ�ţţ�����A�����������ţţǰ��C����ţţͬʱ��������ţţ��Խ��嵽���յ�B��ʱ����Ϣ��100�������ԭ�ٷ���A�أ�����嵽���յ�B����������ԭ���ٶȵ�3.2�������ܣ��������ͬʱ����A�أ����˾�B�ص�·�̼�Ϊy���ף�������ܲ�ʱ���Ϊx���룩��y��x�ĺ�����ϵ��ͼ��ʾ����ţţ�ͷ���һ������ʱ���Ǿ�A��_____�ף�
���𰸡�480
��������
����ͼ�����ţţ���ٶ�,����ʱ���ϵ��������ٶ�,����������ʱ·��֮��Ĺ�ϵ���������һ������ʱ����ʱ��,���������һ������ʱ�ľ���.
�⣺ţţ���ٶ�Ϊ��800����300-100��=4��/��,
�����C��B���ٶ�Ϊx��/��,
������ã�![]()
��ã�x=1.5��/��,������x=1.5��ԭ���̵ĸ�,
������ţţ��һ������ʱ��Ϊt��,
4t=1.5t+(800-500)
��ã�t=120,
��ţţ�ͷ���һ������ʱ���Ǿ�A��ľ����ǣ�4��120=480��,
�ʴ�Ϊ480.

��ϰ��ϵ�д�
 53���ò�ϵ�д�
53���ò�ϵ�д�
�����Ŀ