题目内容
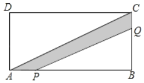
【题目】如图,在矩形ABCD中,AB=10cm,BC=5cm,点P,点Q分别以2cm/s和1cm/s的速度从A,B沿AB,BC方向运动.设t秒(t≤5)时,△PBQ的面积为y.
(1)试写出y与t的函数关系式.
(2)当t为何值时,S△PBQ=6cm2?
(3)在P、Q运动过程中,四边形APQC的面积是否有最小值?如果有,直接写出S四边形APQC= .
【答案】(1)y=﹣t2+5t(2)当t为2秒或3秒时,S△PBQ=6cm2(3)18.75cm2
【解析】
(1)根据题意求出BQ,PB的长度即可列出函数关系式.
(2)把y=6带入函数解析式解出t.
(3)将y的解析式配方后求出△PBQ面积最大值,从而得到四边形APQC面积最小值.
(1)∵四边形ABCD是矩形,AB=10cm,BC=5cm,
根据题意,AP=2t,BQ=t,
∴PB=10﹣2t,
∵S△PBQ=![]() PBQB,
PBQB,
∴y=﹣t2+5t,
(2)把y=6cm2代入解析式,可得:6=﹣t2+5t,
解得:t1=2,t2=3,
答:当t为2秒或3秒时,S△PBQ=6cm2;
(3)∵y=﹣t2+5t=﹣(t﹣2.5)2+6.25,
∴当t=2.5时,y有最大值,最大值为6.25,
∴△PBQ的面积的最大值为6.25cm2,所以四边形APQC的面积此时最小,S四边形APQC=![]() cm2,
cm2,
故答案为:18.75cm2

练习册系列答案
相关题目