题目内容
【题目】如图,在Rt△ABC中,∠C=90°,把Rt△ABC绕着B点逆时针旋转,得到Rt△DBE,点E在AB上,连接AD.
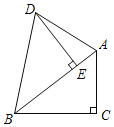
(1)若BC=8,AC=6,求△ABD的面积;
(2)设∠BDA=x°,求∠BAC的度数(用含x的式子表示).
【答案】(1)30; (2)(2x-90)°.
【解析】
(1)根据勾股定理求AB,根据旋转性质得DE=AC=6,根据三角形面积公式可求解;(2)把Rt△ABC绕着B点逆时针旋转,得到Rt△DBE,∠DBA=∠ABC,DB=AB,设∠DBA=∠ABC,DB=AB,根据三角形内角和得∠ABD=180°-2x°=∠ABC,故∠BAC=90°-(180°-2x°).
解:(1)∵∠C=90°,BC=8,AC=6,
∴AB=![]() =10,
=10,
∵把Rt△ABC绕着B点逆时针旋转,得到Rt△DBE,
∴DE=AC=6,
∴S△ABD=![]() AB×DE=
AB×DE=![]() ×6×10=30;
×6×10=30;
(2)∵把Rt△ABC绕着B点逆时针旋转,得到Rt△DBE,
∴∠DBA=∠ABC,DB=AB,
∴设∠BDA=∠BAD=x°,
∵∠ABD=180°-∠BDA-∠BAD,
∴∠ABD=180°-2x°=∠ABC,
∵∠BAC=90°-∠ABC,
∴∠BAC=90°-(180°-2x°)=(2x-90)°

练习册系列答案
相关题目