题目内容
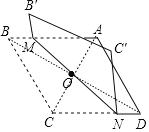
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为( )
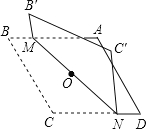
A. 7 B. 6 C. 5 D. 4
【答案】D
【解析】连接AC、BD,如图,利用菱形的性质得OC=![]() AC=3,OD=
AC=3,OD=![]() BD=4,∠COD=90°,再利用勾股定理计算出CD=5,接着证明△OBM≌△ODN得到DN=BM,然后根据折叠的性质得BM=B'M=1,从而有DN=1,于是计算CD﹣DN即可.
BD=4,∠COD=90°,再利用勾股定理计算出CD=5,接着证明△OBM≌△ODN得到DN=BM,然后根据折叠的性质得BM=B'M=1,从而有DN=1,于是计算CD﹣DN即可.
【解答】解:连接AC、BD,如图,
∵点O为菱形ABCD的对角线的交点,
∴OC=![]() AC=3,OD=
AC=3,OD=![]() BD=4,∠COD=90°,
BD=4,∠COD=90°,
在Rt△COD中,CD=![]() =5,
=5,
∵AB∥CD,
∴∠MBO=∠NDO,
在△OBM和△ODN中 ,
,
∴△OBM≌△ODN,
∴DN=BM,
∵过点O折叠菱形,使B,B′两点重合,MN是折痕,
∴BM=B'M=1,
∴DN=1,
∴CN=CD﹣DN=5﹣1=4.
故选:D.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
【题目】某体育运动学校准备在甲、已两位射箭选手中选出成绩比较稳定的一人参加集训,两人各射击了5箭,已知他们的总成绩(单位:环)相同,如下表所示:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)试求出表中a的值;
(2)请你通过计算,从平均数和方差的角度分析,谁将被选中.
[注:平均数x=![]() ;方差
;方差![]() ].
].