题目内容
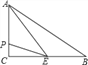
【题目】如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
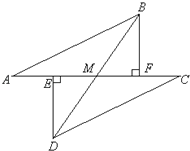
(1)试猜想DE与BF的关系,并证明你的结论;
(2)求证:MB=MD.
【答案】(1)BF=DE;(2)证明见解析
【解析】
试题分析:(1)根据DE⊥AC,BF⊥AC可以证明DE∥BF;再求证Rt△ABF≌Rt△CDE可得BF=DE,即可解题;
(2)根据(1)中结论可证△DEM≌△BFM,即可解题.
解:(1)DE=BF,且DE∥BF,
证明:∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°.
∴DE∥BF,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在Rt△ABF和Rt△CDE中,
![]() ,
,
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE;
(2)在△DEM和△BFM中,
 ,
,
∴△DEM≌△BFM(AAS),
∴MB=MD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目