题目内容
【题目】如图,已知正方形ABCD的边长为6厘米,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由点C向点D运动,设运动时间为t秒。
(1)若点Q的运动速度与点P的运动速度相等,经过2秒后,EP与PQ有什么关系?请说明理由。
(2)若点Q的运动速度与点P的运动速度不相等,则当t为何值时,能使得△EPB与△CQP全等?此时点Q的运动速度为多少?

【答案】(1)EP=PQ,理由见解析;(2)点P,Q运动的时间为![]() 秒,点Q的运动速度为
秒,点Q的运动速度为![]() 厘米/秒.
厘米/秒.
【解析】
(1)根据SAS可判定全等,即可得EP=PQ;
(2)由于点Q的运动速度与点P的运动速度不相等,而运动时间相同,所以BP≠CQ.又△BPE与△CQP全等,则有BP=PC=![]() BC=3厘米,CQ=BE=2厘米,由BP=3厘米求出运动时间,再根据速度=路程÷时间,即可得出点Q的速度.
BC=3厘米,CQ=BE=2厘米,由BP=3厘米求出运动时间,再根据速度=路程÷时间,即可得出点Q的速度.
(1)EP=PQ,
理由:如图,
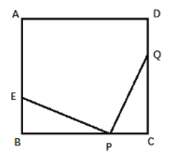
∵点Q的运动速度与点P的运动速度相等,且t=2秒,
∴BP=CQ=2×2=4厘米,
∵AB=BC=6厘米,AE=4厘米,
∴BE=CP=2厘米,
∵四边形ABCD是正方形,
∴在Rt△BPE和Rt△CQP中,
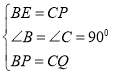 ,
,
∴Rt△BPE≌Rt△CQP,
∴EP=PQ;
(2)∵点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△CQP全等,只要BP=PC=3厘米,CQ=BE=2厘米,即可.
∴点P,Q运动的时间t=![]() =
=![]() (秒),
(秒),
此时点Q的运动速度为VQ=![]() =
=![]() =
=![]() (厘米/秒).
(厘米/秒).

练习册系列答案
相关题目