题目内容
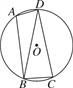
【题目】如图，已知四边形ABCD内接于圆O，连接BD，∠BAD＝105°，∠DBC＝75°.
(1)求证：BD＝CD；
(2)若圆O的半径为3，求
的长．
【答案】（1）证明见解析；（2）π.
【解析】试题分析： 
根据圆内接四边形的对角互补，∠DCB＋∠BAD＝180°，即可求出
的度数，得出
，根据等角对等边即可证明.
求出
的度数，根据弧长公式计算即可.
试题解析：
证明：∵四边形ABCD内接于圆O，
∴∠DCB＋∠BAD＝180°.
∵∠BAD＝105°，
∴∠DCB＝180°－105°＝75°.
∵∠DBC＝75°，
∴∠DCB＝∠DBC＝75°，
∴BD＝CD；
（2）∵∠DCB＝∠DBC＝75°，
∴∠BDC＝30°，
由圆周角定理，得
的度数为60°，
故
的长为： 
练习册系列答案
相关题目
【题目】某种蔬菜的价格随季节变化如下表，根据表中信息，下列结论错误的是（ ）
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
价格 | 5.00 | 5.50 | 5.00 | 4.80 | 2.00 | 1.50 | 1.00 | 0.90 | 1.50 | 3.00 | 2.50 | 3.50 |
A. 
是自变量，
是因变量
B. 2月份这种蔬菜价格最高，为5.50元/千克
C. 2-8月份这种蔬菜价格一直在下降
D. 8-12月份这种蔬菜价格一直在上升
