题目内容
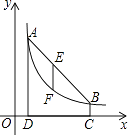
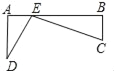
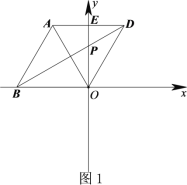
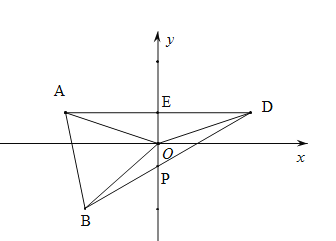
【题目】在平面直角坐标系xOy中,△![]() 为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD,其中AD,BD分别交y轴于点E,P.
为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD,其中AD,BD分别交y轴于点E,P.
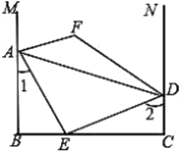
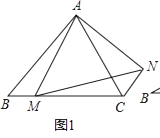
(1)如图1,若点B在x轴的负半轴上时,直接写出![]() 的度数;
的度数;
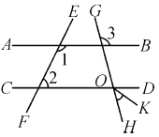
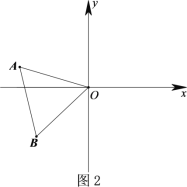
(2)如图2,将△![]() 绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为
绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为![]() ,60<
,60<![]() <90,依题意补全图形,并求出
<90,依题意补全图形,并求出![]() 的度数;(用含
的度数;(用含![]() 的式子表示)
的式子表示)
(3)在第(2)问的条件下,用等式表示线段BP,PE,PO之间的数量关系.(直接写出结果)
【答案】(1)30°;(2)作图见解析,∠BDO=α-60°;(3)2PE=BP+PO.
【解析】
(1)根据轴对称的性质和等边三角形的性质即可得出结论;
(2)由轴对称的性质和等边三角形的性质得出∠BOD=300°﹣2α.在△BOD中根据等腰三角形的性质和三角形内角和定理即可得出结论;
(3)过A作AQ∥EP交DB的延长线于Q,连接AP.由(2)得:∠OBD=∠BDO=α﹣60°.
通过证明△AOP≌△ABQ,得到AP=AQ,OP=QB,∠OAP=∠BAQ,BP+OP=BP+QB=QP.
通过证明△AQP是等边三角形,得出AQ=PQ=AP=BP+OP,∠QAP=60°,即可得到∠PAE=30°,由30°角所对直角边等于斜边的一半即可得到AP=2EP,从而得到结论.
(1)30°.理由如下:
∵A与D关于y轴对称,∴y轴是线段AD的垂直平分线,∴AO=DO,∠AOE=∠DOE.
∵△ABO是等边三角形,∴AB=BO=AO,∠AOB=60°,∴∠AOE=30°,∴∠DOE=30°,∴∠BOD=60°+30°+30°=120°.
∵BO=AO=DO,∴∠BDO=∠OBD=![]() (180°﹣∠BOD)=30°.
(180°﹣∠BOD)=30°.
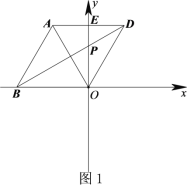
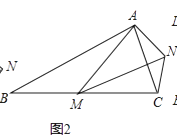
(2)正确画出图形.
∵∠AOE=∠DOE=α,∠AOB=60°,∴∠BOD=360°﹣2α﹣60°=300°﹣2α.
∵BO=BD,∴∠OBD=∠ODB,∴∠BDO=![]() (180°﹣∠BOD)=α﹣60°.
(180°﹣∠BOD)=α﹣60°.
(3)2PE=BP+PO.理由如下:
过A作AQ∥EP交DB的延长线于Q,连接AP.由(2)得:∠OBD=∠BDO=α﹣60°.
∵△ABO是等边三角形,∴AB=BO=AO,∠ABO=∠AOB=∠BAO=60°,∴∠ABQ=180°﹣60°﹣∠OBD=120°﹣(α﹣60°)=180°﹣α.
∵∠AOE=α,∴∠AOP=180°﹣α,∴∠AOP=∠ABQ.
∵AQ∥EP,∴∠Q=∠EPD.
∵∠APE=∠DPE,∴∠APO=∠Q.
在△AOP和△ABQ中,∵∠AOP=∠ABQ,∠APO=∠Q,AO=AB,∴△AOP≌△ABQ,∴AP=AQ,OP=QB,∠OAP=∠BAQ,∴BP+OP=BP+QB=QP.
∵∠BAO=∠BAP+∠OAP=60°,∴∠BAP+∠BAQ=∠PAQ=60°.
∵AQ=AP,∴△AQP是等边三角形,∴AQ=PQ=AP=BP+OP.
∵AQ∥EP,∴∠APE=∠QAP=60°.
∵∠AEP=90°,∴∠PAE=30°,∴AP=2EP,∴2EP=BP+OP.