题目内容
【题目】已知二次函数y=x2﹣x﹣6.
(1)画出函数的图象;
(2)观察图象,指出方程x2﹣x﹣6=0的解及不等式x2﹣x﹣6>0解集;
(3)求二次函数的图象与坐标轴的交点所构成的三角形的面积.
【答案】(1)图形见解析
(2)x<﹣2或x>3;
(3)三角形的面积为15.
【解析】试题分析:(1)由抛物线开口方向,与x轴交点坐标,顶点坐标画出图象;
(2)根据图象直接写出答案;
(3)由三角形的面积公式进行解答.
试题解析:(1)函数图象如下:
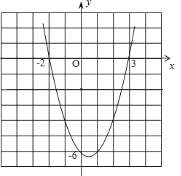
(2)由抛物线解析式y=x2﹣x﹣6知,抛物线与x轴的交点坐标是(3,0),(﹣2,0),
方程x2﹣x﹣6=0的解是x1=﹣2,x2=3;
不等式x2﹣x﹣6>0的解集为x<﹣2或x>3;
(3)如图所示:抛物线与坐标轴所构成的三角形面积是:![]() ×|﹣2﹣3|×|﹣6|=15.
×|﹣2﹣3|×|﹣6|=15.
即抛物线与坐标轴所构成的三角形面积是15三角形的面积为15.

练习册系列答案
相关题目