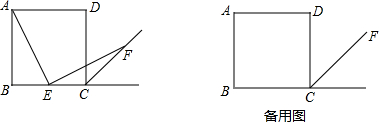题目内容
如图,四边形ABCD内接于半圆O,AB是直径.
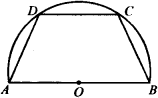
(1)请你添加一个条件,使图中的四边形ABCD成等腰梯形,这个条件是________(只需填一个条件).
(2)如果CD=![]() AB,请你设计一种方案,使等腰梯形ABCD分成面积相等的三部分,并给予证明.
AB,请你设计一种方案,使等腰梯形ABCD分成面积相等的三部分,并给予证明.
答案:
解析:
解析:
|
(1)∠A=∠B(或AD=BC,或DC∥AB,或∠D+∠A=180°) (2)如图,连结OD,OC,则S△AOD=S△BOC=S△COD= 证明:∵CD∥AB,CD= ∴∠CDO=∠AOD,CD=AO, ∴△CDO≌△AOD,同理,△CDO≌△BOC, ∴S△AOD=S△BOC=S△CDO= |

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
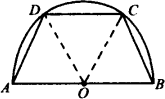
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.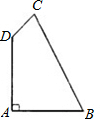 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.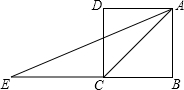 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.