Question

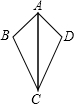
如图所示，在平行四边形ABCD中，AE⊥BD，FC⊥BD，垂足分别为E，F．
（1）写出图中所有的全等三角形；
（2）选择（1）中的任意一对全等三角形进行证明．

Answer 1

（1）①△ABD≌△CDB②△ABE≌△CDF③△AED≌△CFB；

（2）①证明△ABD≌△CDB．
证明：∵四边形ABCD是平行四边形，
∴AB=CD，AD=CB，
∵BD=DB，
∴△ABD≌△CDB．
②证明△ABE≌△CDF．
证明：∵AE⊥BD，CF⊥BD，
∴∠AEB=∠CFD=90°．
∵ABCD是平行四边形，
∴AB∥CD且AB=CD．
∴∠ABE=∠CDF．
∴△ABE≌△CDF．
③证明△AED≌△CFB．
证明：∵AE⊥BD，CF⊥BD，
∴∠AED=∠CFB=90°．
∵ABCD是平行四边形，
∴AD∥CB且AD=CB．
∴∠ADE=∠CBF．
∴△AED≌△CFB．