ĢāÄæÄŚČŻ
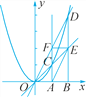
”¾ĢāÄæ”æČēĶ¼£¬ŌŚxÖįÉĻÓŠĮ½µćA(m£¬0)£¬B(n£¬0)(n>m>0)£¬·Ö±š¹żµćA£¬B×÷xÖįµÄ“¹
Ļß½»Å×ĪļĻßy£½x2ÓŚµćC£¬D£¬Ö±ĻßOC½»Ö±ĻßBDÓŚµćE£¬Ö±ĻßOD½»Ö±ĻßACÓŚµćF.µćE£¬FµÄׯ×ų±ź·Ö±šĪŖyE£¬yF.
(1)ĢŲĄżĢ½¾æ(ĢīæÕ)£ŗ
µ±m£½1£¬n£½2Ź±£¬yE£½____£¬yF£½____£»
µ±m£½3£¬n£½5Ź±£¬yE£½____£¬yF£½____£®
(2)¹éÄÉÖ¤Ć÷£ŗ¶ŌČĪŅām,n(n>m>0)£¬²ĀĻėyEÓėyFµÄ“󊔹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ²ĀĻė£®
(3)ĶŲÕ¹Ó¦ÓĆ£ŗĮ¬½įEF£¬AE£¬µ±SĖıߊĪOFEB£½3S”÷OFEŹ±£¬Ö±½ÓŠ“³ömÓėnµÄ¹ŲĻµ¼°ĖıߊĪOFEAµÄŠĪד£®
”¾“š°ø”æ(1) µ±m£½1£¬n£½2Ź±£¬yE£½__2__£¬ ![]() £½__2__£»µ±m£½3£¬n£½5Ź±£¬
£½__2__£»µ±m£½3£¬n£½5Ź±£¬ ![]() £½__15__£¬yF£½__15__£®
£½__15__£¬yF£½__15__£®
(2) ![]() =
=![]() .Ö¤Ć÷¼ū½āĪö£®
.Ö¤Ć÷¼ū½āĪö£®
(3) n£½2m,ĖıߊĪOFEAĪŖĘ½ŠŠĖıߊĪ.
”¾½āĪö”æ·ÖĪö£ŗ£Ø1£©ŅŃÖŖA”¢BµÄ×ų±ź£¬øł¾ŻÅ×ĪļĻߵĽāĪöŹ½£¬ÄܵƵ½C”¢DµÄ×ų±ź£¬½ų¶ųÄÜĒó³öÖ±ĻßOC”¢ODµÄ½āĪöŹ½£¬Ņ²¾ĶÄÜµĆ³öE”¢FĮ½µćµÄ×ų±ź£¬ŌŁ½ųŠŠ±Č½Ļ¼“æÉ£®£Ø2£©ŅŃÖŖA”¢BµÄ×ų±ź£¬øł¾ŻÅ×ĪļĻߵĽāĪöŹ½£¬ÄܵƵ½C”¢DµÄ×ų±ź£¬½ų¶ųÄÜĒó³öÖ±ĻßOC”¢ODµÄ½āĪöŹ½£¬Ņ²¾ĶÄÜµĆ³öE”¢FĮ½µćµÄ×ų±ź£¬ŌŁ½ųŠŠ±Č½Ļ¼“æÉ£®£Ø3£©ĖıߊĪOFEAµÄĆ껿æÉ·Ö×÷”÷OEF”¢”÷OEAĮ½²æ·Ö£¬øł¾Żøų³öµÄĖıߊĪŗĶ”÷OFEµÄĆ껿±ČĄż¹ŲĻµ£¬ÄÜÅŠ¶Ļ³öEF”¢OAµÄ±ČĄż¹ŲĻµ£¬½ų¶ųµĆ³öm”¢nµÄ±ČĄż¹ŲĻµ£¬ŌŁ¶ŌĖıߊĪOFEAµÄŠĪד½ųŠŠÅŠ¶Ø£®
±¾Ģā½āĪö£ŗ
(1) µ±m£½1£¬n£½2Ź±£¬yE£½__2__£¬yF£½__2__£»µ±m£½3£¬n£½5Ź±£¬yE£½__15__£¬yF£½__15__.
(2)”ßµćCĪŖÅ×ĪļĻßy£½x2ÉĻµÄµć£¬AC”ĶxÖį£¬”ąxC£½xA£½m£¬”ąµćC(m£¬m2)£®
Ņ×ĒóµĆÖ±ĻßyOC£½mx£¬
ÓÖ”ßxE£½n£¬”ąyE£½mn.
Ķ¬Ąķ£¬µćD(n£¬n2)£¬Ņ×ĒóµĆÖ±ĻßyOD£½nx£¬
”ąyF£½nm£½mn.”ąyE£½yF.
(3)”ßyE£½yF£¬AF”ĶxÖį£¬BE”ĶxÖį£¬
”ąAF£½BE£¬AF”ĪBE£¬
”ąĖıߊĪABEFĪŖĘ½ŠŠĖıߊĪ£¬
”ąEF”ĪOB£¬EF£½AB£½n£m.
”ąSĖıߊĪOFEB£½![]() (n£m£«n)”¤yE£½
(n£m£«n)”¤yE£½![]() (2n£m)”¤yE£¬S”÷OFE£½
(2n£m)”¤yE£¬S”÷OFE£½ ![]() (n£m)”¤yE.
(n£m)”¤yE.
”ßSĖıߊĪOFEB£½3S”÷OFE£¬
”ą![]() (2n£m)”¤yE£½3”Į
(2n£m)”¤yE£½3”Į![]() (n£m)”¤yE£¬
(n£m)”¤yE£¬
”ą2n£m£½3(n£m)£¬”ąn£½2m.
“ĖŹ±EF£½n£m£½2m£m£½m£½OA£¬
”ąEFĘ½ŠŠĒŅµČÓŚOA£¬”ąĖıߊĪOFEAĪŖĘ½ŠŠĖıߊĪ£®

 ѧĮ·æģ³µµĄæŚĖćŠÄĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø
ѧĮ·æģ³µµĄæŚĖćŠÄĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø