题目内容
【题目】抛物线y＝ax2(a≠0)与直线y＝4x－3交于点A(m，1)．
(1)求点A的坐标及抛物线的函数表达式．(2)写出抛物线的开口方向、顶点坐标和对称轴．
(3)写出抛物线y＝ax2与直线y＝4x－3的另一个交点B的坐标．
【答案】(1) 点A(1，1), y＝x2; (2) 开口向上，顶点坐标为(0，0)，对称轴为y轴;
(3) 点B(3，9)．
【解析】分析：（1）将A坐标代入直线解析式求出m的值，确定出A坐标，将A坐标代入抛物线解析式中求出a的值，即可确定出抛物线解析式；（2）根据a的正负判断出开口方向，找出顶点坐标与对称轴即可；（3）联立两函数解析式求出另一个交点B即可．
本题解析：
(1)∵点A(m，1)在y＝4x－3上，
∴1＝4m－3，∴m＝1，∴点A(1，1)．
又∵点A(1，1)在抛物线y＝ax2上，
∴1＝a·12，∴a＝1，∴y＝x2.
(2)开口向上，顶点坐标为(0，0)，对称轴为y轴．
(3)根据题意，得
解得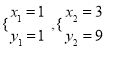
∴点B(3，9)．
练习册系列答案
相关题目
