题目内容
【题目】如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.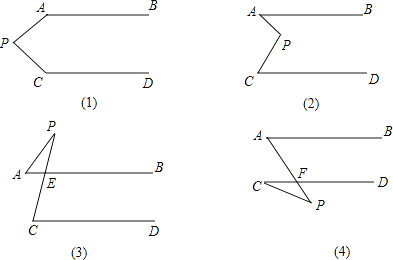
(1);
(2);
(3);
(4) .
【答案】
(1)∠APC+∠PAB+∠PCD=360°
(2)∠APC=∠BAP+∠DCP
(3)∠DCP=∠BAP+∠APC
(4)∠BAP=∠C+∠P
【解析】解:(1)连接AC,
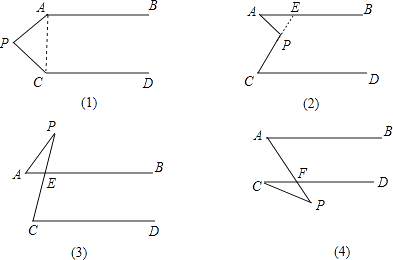
∵AB∥CD,
∴∠BAC+∠DCA=180°,
∵在△APC中,∠APC+∠PAC+∠PCA=180°,
∴∠APC+∠PAC+∠PCA+∠BAC+∠DCA=360°,
即∠APC+∠PAB+∠PCD=360°,
所以答案是:∠APC+∠PAB+∠PCD=360°;
⑵延长CP交AB于E,
∵AB∥CD,
∴∠DCP=∠AEP,
∵∠APC=∠BAP+∠AEP,
∴∠APC=∠BAP+∠DCP,
所以答案是:∠APC=∠BAP+∠DCP;
⑶∵AB∥CD,
∴∠DCP=∠BEP,
∵∠BEP=∠BAP+∠APC,
∴∠DCP=∠BAP+∠APC,
所以答案是:∠DCP=∠BAP+∠APC;
⑷∵AB∥CD,
∴∠BAP=∠DFP,
∵∠DFP=∠C+∠P
∴∠BAP=∠C+∠P
所以答案是∠BAP=∠C+∠P.
【考点精析】根据题目的已知条件,利用平行线的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

【题目】某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如表:
小组 | 研究报告 | 小组展示 | 答辩 |
甲 | 91 | 80 | 78 |
乙 | 81 | 74 | 85 |
丙 | 79 | 83 | 90 |
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?