题目内容
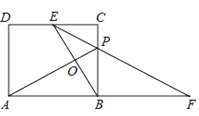
【题目】如图,在钝角三角形![]() 中,分别以
中,分别以![]() 和
和![]() 为斜边向
为斜边向![]() 的外侧作等腰直角三角形
的外侧作等腰直角三角形![]() 和等腰直角三角形
和等腰直角三角形![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,取
,取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论有( )
.其中正确结论有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
【答案】D
【解析】
①首先根据D是BC中点,N是AC中点N,可得DN是△ABC的中位线,判断出DN=![]() AB;然后判断出EM=
AB;然后判断出EM=![]() AB,即可判断出EM=DN;
AB,即可判断出EM=DN;
②首先根据DN∥AB,可得△CDN∽ABC;然后根据DN=![]() AB,可得S△CDN=
AB,可得S△CDN=![]() S△ABC,所以S△CDN=
S△ABC,所以S△CDN=![]() S四边形ABDN,据此判断即可.
S四边形ABDN,据此判断即可.
③首先连接MD、FN,判断出DM=FN,∠EMD=∠DNF,然后根据全等三角形判定的方法,判断出△EMD≌△DNF,即可判断出DE=DF.
④首先判断出![]() =sin45°=
=sin45°=![]() ,DM=
,DM=![]() FA,∠EMD=∠EAF,根据相似三角形判定的方法,判断出△EMD∽△∠EAF,即可判断出∠MED=∠AEF,然后根据∠MED+∠AED=45°,判断出∠DEF=45°,再根据DE=DF,判断出∠DFE=45°,∠EDF=90°,即可判断出DE⊥DF.
FA,∠EMD=∠EAF,根据相似三角形判定的方法,判断出△EMD∽△∠EAF,即可判断出∠MED=∠AEF,然后根据∠MED+∠AED=45°,判断出∠DEF=45°,再根据DE=DF,判断出∠DFE=45°,∠EDF=90°,即可判断出DE⊥DF.
解:∵D是BC中点,N是AC中点,
∴DN是△ABC的中位线,
∴DN∥AB,且DN=![]() AB;
AB;
∵三角形ABE是等腰直角三角形,EM平分∠AEB交AB于点M,
∴M是AB的中点,
∴EM=![]() AB,
AB,
又∵DN=![]() AB,
AB,
∴EM=DN,
∴结论①正确;
∵DN∥AB,
∴△CDN∽ABC,
∵DN=![]() AB,
AB,
∴S△CDN=![]() S△ABC,
S△ABC,
∴S△CDN=![]() S四边形ABDN,
S四边形ABDN,
∴结论②正确;
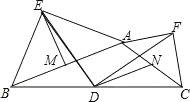
如图1,连接MD、FN,
∵D是BC中点,M是AB中点,
∴DM是△ABC的中位线,
∴DM∥AC,且DM=![]() AC;
AC;
∵三角形ACF是等腰直角三角形,N是AC的中点,
∴FN=![]() AC,
AC,
又∵DM=![]() AC,
AC,
∴DM=FN,
∵DM∥AC,DN∥AB,
∴四边形AMDN是平行四边形,
∴∠AMD=∠AND,
又∵∠EMA=∠FNA=90°,
∴∠EMD=∠DNF,
在△EMD和△DNF中,
EM=DN,∠EMD=∠DNF,MD=NF,
∴△EMD≌△DNF,
∴DE=DF,
∴结论③正确;
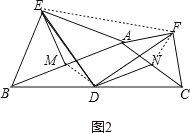
如图2,连接MD,EF,NF,
∵三角形ABE是等腰直角三角形,EM平分∠AEB,
∴M是AB的中点,EM⊥AB,
∴EM=MA,∠EMA=90°,∠AEM=∠EAM=45°,
∴![]() =sin45°=
=sin45°=![]() ,
,
∵D是BC中点,M是AB中点,
∴DM是△ABC的中位线,
∴DM∥AC,且DM=![]() AC;
AC;
∵三角形ACF是等腰直角三角形,N是AC的中点,
∴FN=![]() AC,∠FNA=90°,∠FAN=∠AFN=45°,
AC,∠FNA=90°,∠FAN=∠AFN=45°,
又∵DM=![]() AC,
AC,
∴DM=FN=![]() FA,
FA,
∵∠EMD=∠EMA+∠AMD=90°+∠AMD,
∠EAF=360°∠EAM∠FAN∠BAC
=360°45°45°(180°∠AMD)
=90°+∠AMD
∴∠EMD=∠EAF,
在△EMD和△∠EAF中,![]() ,∠EMD=∠EAF,
,∠EMD=∠EAF,
∴△EMD∽△∠EAF,
∴∠MED=∠AEF,
∵∠MED+∠AED=45°,
∴∠AED+∠AEF=45°,
即∠DEF=45°,
又∵DE=DF,
∴∠DFE=45°,
∴∠EDF=180°45°45°=90°,
∴DE⊥DF,
∴结论④正确.
∴正确的结论有4个:①②③④.
故选:D.

 名校课堂系列答案
名校课堂系列答案