Question

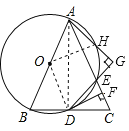
【题目】如图，在△ABC中，AB＝AC＝10，以AB为直径的OO与BC相交于点D，与AC相交于点E，DF⊥AC，垂足为F，连接DE，过点A作AG⊥DE，垂足为G，AG与⊙O交于点H．

（1）求证：DF是⊙O的切线；

（2）若∠CAG＝25°，求弧AH的长；

（3）若tan∠CDF＝，求AE的长；

Answer 1

【答案】（1）证明见解析（2）（3）6

【解析】

（1）连接OD、AD，根据圆周角定理得到∠ADB＝90°，求得OD∥AC，根据平行线的性质得到OD⊥DF，根据切线的判定定理即可得到结论；

（2）连接OH，根据三角形的内角和得到∠AEG＝65°，求得∠B＝∠AEG＝65°，求得∠AOH＝30°，根据弧长公式即可得到结论；

（3）根据余角的性质得到∠CAD＝∠CDF，求出tan∠CAD＝tan∠CDF＝，根据勾股定理得到CD＝2，根据相似三角形的性质得到CF＝2，于是得到结论．

（1）证明：连接OD、AD，

AB是⊙O的半径，

∴∠ADB＝90°，

∵AB＝AC，

∵点D是BC的中点，O是AB的中点，

∴OD∥AC，

∵DF⊥AC，

∴OD⊥DF，

∵OD是⊙O的半径，

DF是⊙O的切线；

（2）解：连接OH，

∵AG⊥DG，∴∠G＝90°，

∵∠CAG＝25°，

∴∠AEG＝65°，

∴∠B＝∠AEG＝65°，

∴∠BAC＝180°﹣65°﹣65°＝50°，

∴∠OAH＝75°，

∴∠AOH＝30°，

∴l弧AH＝；

（3）解：∵∠CAD+∠C＝90°，∠CDF+∠C＝90°，

∴∠CAD＝∠CDF，

∴tan∠CAD＝tan∠CDF＝，

∴AD＝2CD，

∴DC2+（2CD）2＝102，

∴CD＝2，

∵△CDF∽△CAD，

∴DC2＝CFAC，

∴CF＝2，

∴CD＝DE，

∵OF⊥AC，

∴EF＝CF＝2，

∴AE＝10﹣2﹣2＝6．