题目内容
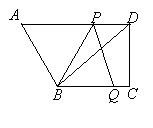
【题目】如图，在直角梯形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21。动点P从点D出发，沿射线DA的方向以每秒2两个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动。设运动的时间为t（秒）．
【1】设△BPQ的面积为S，求S与t之间的函数关系式
【2】当线段PQ与线段AB相交于点O，且2AO＝OB时，求t的值．
【3】当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？
【4】是否存在时刻t，使得PQ⊥BD？若存在，求出t的值；若不存在，请说明理由．
【答案】
【1】s=×12×(16t)=966t
【2】由题意得 △AOP∽△BOQ ∴== ∴BQ=2AP
∴16t=2(2t21) ∴t=
【3】①若BQ=PQ 则 t2+122=(16t)2 得t=
②若BP=BQ 则（162t）2+122=(16t)2 得3t232t+144=0 ∵△=3224×3×144＜0
∴3t232t+144=0无解 ∴BP≠BQ
③若BP=PQ 则 （162t）2+122= t2+122 ∴t=或t=16(不合题意舍去)
综上所述当t=或t=时，以B，P，Q三点为顶点的三角形是等腰三角形
【4】存在时刻t，使得PQBD
过Q作QEAD，垂足为E，由PQBD可知△PQE∽△DBC
∴=
∴ = ∴t=9
所以，当t=9时，PQBD。
【解析】略
金钥匙试卷系列答案
【题目】某商场经营一种商品，进价是每千克30元，根据市场调查发现，每日的销售量
（千克）与售价
（元/千克）满足一次函数关系．下表记录的是某两日的有关数据：
| 35 | 40 |
| 850 | 800 |
（1）求与的函数关系式（不求自变量的取值范围）；
（2）在销售过程中销售单价不低于成本价，且不高于80元，某日该商场出售这种商品获得了14000元的利润，求该商品的售价？
（3）若某日该商场这种商品的销售量不少于500千克，求这一天该商场销售这种商品获得的最大利润为多少元？
