题目内容
【题目】如图,在下列14×7的网格中,横、纵坐标均为整点的数叫做格点,例如A(-6,0)、B(-3,4)都是格点.
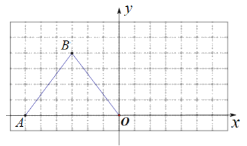
(1)直接写出△ABO的形状;
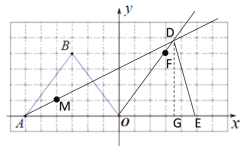
(2)要求在下图中仅用无刻度的直尺作图:将△ABO绕点O顺时针旋转得△DEO,且点B的对应点E落在x轴正半轴上.操作如下:
第一步:在x正半轴上找一个格点E,使OE=OB;
第二步:找一个格点F,使∠EOF=∠AOB;
第三步:找一个格点M,作直线长AM交直线OF于D,连DE,则△DEO即为所作出的图形.
请你按步骤完成作图,并直接写出直线AM的解析式.
【答案】(1)等腰三角形;(2)见解析,![]()
【解析】
(1)根据勾股定理求出OB和AB即可得出结论;
(2)根据作图步骤补全图形,利用锐角三角函数和全等三角形即可说明,然后利用待定系数法求直线AM的解析式即可.
解:(1)等腰三角形,理由如下
由坐标可知:OB=![]() ,AB=
,AB=![]() ,OA=6
,OA=6
∴OB=AB
∴△ABO为等腰三角形
(2)第一步:在x正半轴上找一个格点E,使OE=OB=5;
第二步:找一个格点F(3,4),此时tan∠EOF=![]() =tan∠AOB,所以∠EOF=∠AOB;
=tan∠AOB,所以∠EOF=∠AOB;
第三步:找一个格点M(-4,1),作直线长AM交直线OF于D,连接DE,过点D作DG⊥x轴于点G
坐标系可知:tan∠DAG=![]() ,tan∠EOF=
,tan∠EOF=![]()
∴![]() ,
,![]()
设DG=4x,则OG=3x,AG=8x
根据勾股定理OD=![]() ,而AO=AG-OG=5x
,而AO=AG-OG=5x
∴OD=OA,
∵OE=OB,∠EOF=∠AOB,OD=OA
∴△OED≌OBA
则△DEO即为所作出的图形.
设直线AM的解析式为y=kx+b
将点A、M的坐标代入,得
![]()
解得:![]()
∴直线AM的解析式为![]()

【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下统计图:

(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为___________度
(2)请补充完整下面的成绩统计分析表:
平均数 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 |
|
乙组 | 1.36 |
|
(3)你认为那组成绩较好?从以上信息中写出两条支持你的选择
(4)从甲、乙两组得9分的学生中抽取两人参加市级比赛,求这两人来自不同组的概率
【题目】某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息解答下列问题:
组别 | 阅读时间 | 频数(人数) |
|
| 8 |
|
| 20 |
|
| 24 |
|
|
|
|
|
|
|
| 4 |
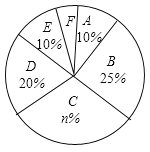
(1)图表中的![]() ______,
______,![]() ______;
______;
(2)扇形统计图中![]() 组所对应的圆心角为______度;
组所对应的圆心角为______度;
(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?