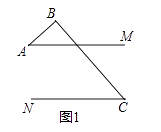题目内容
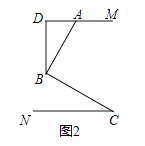
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向过点A的直线作垂线,垂足分别为点E,F.
(1)如图(1),过A的直线与斜边BC不相交时,求证:①△ABE≌△CAF; ②EF=BE+CF 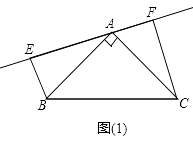
(2)如图(2),过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,试求EF的长. 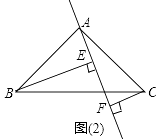
【答案】
(1)证明:
①∵BE⊥EF,CF⊥EF,
∴∠AEB=∠CFA=90°,
∴∠EAB+∠EBA=90°,
∵∠BAC=90°,
∴∠EAB+∠FAC=90°,
∴∠EBA=∠FAC,
在△AEB与△CFA中

∴△ABE≌△CAF(AAS),
②∵△ABE≌△CAF,
∴EA=FC,EB=FA,
∴EF=AF+AE
=BE+CF
(2)解:∵BE⊥AF,CF⊥AF
∴∠AEB=∠CFA=90°
∴∠EAB+∠EBA=90°
∵∠BAC=90°
∴∠EAB+∠FAC=90°
∴∠EBA=∠FAC,
在△AEB与△CFA中

∴△ABE≌△CAF(AAS),
∴EA=FC,EB=FA,
∴EF=FA﹣EA=EB﹣FC=10﹣3=7
【解析】(1)①由条件可求得∠EBA=FAC,利用AAS可证明△ABE≌△CAF;②利用全等三角形的性质可得EA=FC,EB=FA,利用线段的和差可证得结论;(2)同(1)可证明△ABE≌△CAF,可证得EF=FA﹣EA,代入可求得EF的长.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目