题目内容
【题目】科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若b反射出的光线n平行于m,且∠1=50°,则∠2= , ∠3=;
(2)在(1)中,若∠1=40°,则∠3= , 若∠1=55°,则∠3=;
(3)由(1)(2)请你猜想:当∠3=时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由.
【答案】
(1)100°;90°
(2)90°;90°
(3)90°
【解析】解:(1.)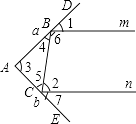
∵∠1=50°,
∴∠4=∠1=50°,
∴∠6=180°﹣50°﹣50°=80°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=100°,
∴∠5=∠7=40°,
∴∠3=180°﹣50°﹣40°=90°,
所以答案是:100°,90°.
(2.)∵∠1=40°,
∴∠4=∠1=40°,
∴∠6=180°﹣40°﹣40°=100°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=80°,
∴∠5=∠7=50°,
∴∠3=180°﹣50°﹣40°=90°;
∵∠1=55°,
∴∠4=∠1=55°,
∴∠6=180°﹣55°﹣55°=70°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=110°,
∴∠5=∠7=35°,
∴∠3=180°﹣55°﹣35°=90°;
所以答案是:90°,90°;
(3.)当∠3=90°时,m∥n,
理由是:∵∠3=90°,
∴∠4+∠5=180°﹣90°=90°,
∵∠1=∠4,∠7=∠5,
∴∠1+∠4+∠5+∠7=2×90°=180°,
∴∠6+∠2=180°﹣(∠1+∠4)+180°﹣(∠5+∠7)=180°,
∴m∥n,
所以答案是:90°.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.