题目内容
【题目】直线:![]() ,与
,与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() :
:![]() ,经过点
,经过点![]() ,且与
,且与![]() 轴的另一个交点为点
轴的另一个交点为点![]() .
.

(1)若![]() ,求此时抛物线的解析式、顶点坐标及点
,求此时抛物线的解析式、顶点坐标及点![]() 坐标;
坐标;
(2)在直线![]() 与抛物线
与抛物线![]() 围成的封闭图形边界上,横、纵坐标均为整数的点称为“神秘点”,求出在(l)的条件下“神秘点”的个数;
围成的封闭图形边界上,横、纵坐标均为整数的点称为“神秘点”,求出在(l)的条件下“神秘点”的个数;
(3)①直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标会变吗?说明理由;
的坐标会变吗?说明理由;
②若抛物线![]() 与直线
与直线![]() 在
在![]() 的范围内有唯一公共点,请直接写出
的范围内有唯一公共点,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,顶点为
,顶点为![]() ,
,![]() ;(2)①不会变,理由见解析;②
;(2)①不会变,理由见解析;②![]() ,
,![]() ,
,![]()
【解析】
(1)将a=1代入一次函数解析式求得点A的坐标,然后将a的值及 A点坐标代入二次函数解析式求得b的值,然后利用配方法和二次函数的性质求二次函数顶点坐标及点C的坐标;
(2)通过联立方程组求得直线与抛物线的交点坐标,从而确定“神秘点”的个数;
(3)①将一次函数变形为![]() ,然后分析无论
,然后分析无论![]() 取何非零实数,
取何非零实数,![]() 恒为0,从而求解;
恒为0,从而求解;
②结合点A坐标求得抛物线的解析式及对称轴,然后分a>0,a<0时结合函数图像讨论求得a的取值范围.
解:(1)若![]() ,
,![]() ,当
,当![]() 时,
时,![]()
∴![]() ,
,![]()
将![]() 代入,可得
代入,可得![]()
∴![]()
∴顶点为![]()
∵点![]() ,点
,点![]() 关于
关于![]() 对称
对称
∴![]()
(2)设直线与抛物线的另一个交点为![]() ,
,
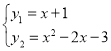 ,
,
解得![]() ,
,![]() ,所以交点为
,所以交点为![]() 和
和![]() ,
,
所以,直线![]() 上神秘点为
上神秘点为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6个,
共6个,
抛物线上神秘点为![]() ,
,![]() ,
,![]() ,
,![]() 共4个,
共4个,
综上,神秘点个数为10;
(1)①不会变,![]() ,
,
当![]() 时,无论
时,无论![]() 取何非零实数,
取何非零实数,![]() 恒为0,
恒为0,
所以,直线永远经过点![]() ,所以点
,所以点![]() 坐标不会改变;
坐标不会改变;
②![]() ,
,![]() ,
,![]()
由①知![]() 恒过
恒过![]()
∴![]() 过
过![]() ∴
∴![]() ∴
∴![]()
∴![]()
![]()
∴与![]() 轴恒交于
轴恒交于![]() ,
,![]()
对称轴为![]() 不变
不变
∵与![]() 在
在![]() 有唯一公共点
有唯一公共点
∴当![]() 时过
时过![]()
![]()
解得![]()
∵开口越小,![]() 越大
越大
∴![]()
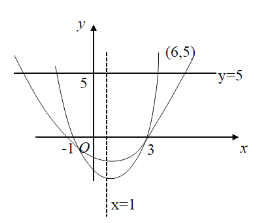
当![]() 时
时
①顶点在![]() 上,顶点为
上,顶点为![]()
![]() ∴
∴![]()
②抛物线恰好过![]()
![]() ∴
∴![]()
∴![]()
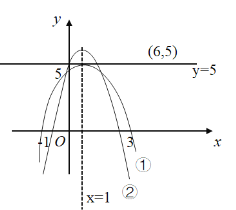
综上![]() ,
,![]() ,
,![]() 时抛物线与
时抛物线与![]() 在
在![]() 有唯一公共点
有唯一公共点

 名校课堂系列答案
名校课堂系列答案【题目】《中学生体质健康标准》规定的等级标准为:90分及以上为优秀,80~89分为良好,60~79分为及格,59分及以下为不及格.某校为了解七、八年级学生的体质健康情况,现从两年级中各随机抽取10名同学进行体质健康检测,并对成绩进行分析.成绩如下:
七年级 | 80 | 74 | 83 | 63 | 90 | 91 | 74 | 61 | 82 | 62 |
八年级 | 74 | 61 | 83 | 91 | 60 | 85 | 46 | 84 | 74 | 82 |
(1)根据上述数据,补充完成下列表格中序号.
整理数据:
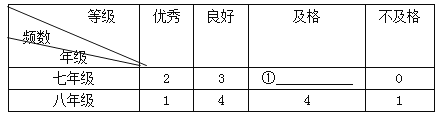
分析数据:
年级 | 平均数 | 众数 | 中位数 |
七年级 | ②_________ | 74 | 77 |
八年级 | 74 | 74 | ③____________ |
(2)该校目前七年级有300人,八年级有200人,试估计两个年级体质健康等级达到优秀的学生共有多少人?
(3)结合上述数据信息,你认为哪个年级学生的体质健康情况更好,并说明理由.