题目内容
【题目】在平行四边形ABCD中，过点A作AE⊥BC于点E，点F在边AD上，且DF=BE，连接DE，CF．
（1）求证：四边形AECF是矩形；
（2）若DE平分∠ADC，AB=5，AD=8，求tan∠ADE的值．
【答案】（1）见解析；（2）
【解析】
（1）证四边形AECF是平行四边形，再证出∠AEC=90°，即可得出结论；
（2）证出∠DEC=∠CDE，得出CD=CE=5，则BE=BC-CE=3，由勾股定理求出AE=4，再由三角函数定义即可得出答案．
解：（1）∵在平行四边形ABCD中
∴AD＝BC，AD∥BC，
又∵DF=BE，
∴AF＝EC
∴四边形AECF为平行四边形
∵∠AEC＝90°
∴平行四边形AECF为矩形
（2）∵DE平分∠ADC，
∴∠ADE＝∠CDE
∵AD∥BC
∴∠ADE＝∠CED
∴∠CDE＝∠CED
∴EC＝DC＝AB＝5
∴BE＝3
在Rt△ABE中，AE＝
＝4
∵在矩形 AECF中
∴∠DAE＝90°
∴tan∠ADE＝
＝
＝
智慧课堂密卷100分单元过关检测系列答案【题目】经过多方努力，北京市2019年在区域空气质量同步改善、气象条件较常年整体有利的情况下，大气环境中细颗粒物（
）等四项主要污染物同比均明显改善对北京市空气质量的有关数据进行收集、整理、描述与分析，下面给出了部分信息：
a．北京市2019年空气质量各级别分布情况如下图（全年无严重污染日）（不完整）：
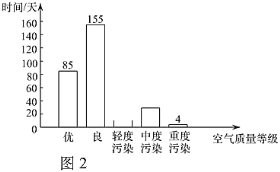
b．北京市2019年大气环境中二氧化硫（
）的年均浓度为4微克/立方米，稳定达到国家二级标准（60微克/立方米）；
，二氧化氮（
）的年均浓度分别为68微克/立方米，37微克/立方米，均首次达到国家二级标准（70微克/立方米，40微克/立方米）；
的年均浓度为
微克立方米，仍是北京市大气主要污染物，超过国家二级标准（35微克/立方米）的20%．
c．北京市2019年大气环境中月均浓度变化情况如下：
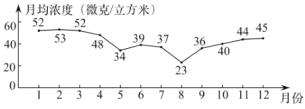
二氧化硫（）月均浓度（单位：微克/立方米）如下（不完整）：
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
月均浓度 | 9 | 6 | 5 | 4 | 3 | 2 | 3 | 3 | 5 | 4 |
（以上数据来源于北京市生态环境局官方网站）
根据以上信，回答下列问题：
（1）北京市2019年空气质量为“轻度污染”天数为（ ）．
A．82 B．92 C．102
（2）的值是______；
（3）北京市2019年大气环境中月均浓度达到国家二级标准的概率为______；
（4）北京市2019年大气环境中月均浓度的众数是4，则中位数是______．
【题目】某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且不高于80元，经市场调查，每天的销售量y（千克）与每千克售价x（元）满足一次函数关系，部分数据如下表：
售价x（元/千克） | 50 | 60 | 70 |
销售量y（千克） | 100 | 80 | 60 |
（1）求y与x之间的函数表达式；
（2）设商品每天的总利润为W（元），则当售价x定为多少元时，厂商每天能获得最大利润？最大利润是多少？
（3）如果超市要获得每天不低于1350元的利润，且符合超市自己的规定，那么该商品每千克售价的取值范围是多少？请说明理由．