题目内容
【题目】(本题满分10分)如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°,请解答下列问题:

(1)求∠CAD的度数;
(2)设AD、BC相交于E,AB、CD的延长线相交于F,求∠AEC、∠AFC的度数;
(3)若AD=6,求图中阴影部分的面积.
【答案】(1)30°;(2)∠AEC=100°,∠AFC=20°;(3)![]() .
.
【解析】试题分析:
(1)根据圆周角定理求出∠ADC、∠ACD的度数,相减即可;
(2)根据三角形的内角和定理求出∠BAC,根据三角形的外角性质求出即可;
(3)连接OC,过O作OQ⊥AC于Q,求出∠AOC的度数,求出高OQ和弦AC,求出扇形和三角形的面积,相减即可.
试题解析:
:(1)∵弧AC=弧AC,
∴∠ADC=∠ABC=60°,
∵AD是直径,
∴∠ACD=90°,
∴∠CAD=180°-∠ACD-∠ADC=30°,
答:∠CAD的度数是30°.
(2)∵∠BAC=180°-∠ABC-∠ACB=70°,
∴∠BAD=∠BAC-∠CAD=70°-30°=40°,
∴∠BCD=∠BAD=40°,
∴∠AEC=∠ADC+∠BCD=100°,
∵∠AFC=∠ABC-∠BCF=60°-40°=20°,
答:∠AEC=100°,∠AFC=20°.
连接OC,过O作OQ⊥AC于Q,
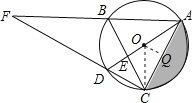
∵∠CAD=30°,AO=3,
∴OQ=![]()
由勾股定理得:AQ=![]()
由垂径定理得:AC=2AQ=![]()
∵∠AOC=2∠ABC=120°,
∴阴影部分的面积是S扇形OAC-S△AOC=![]() .
.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
