题目内容
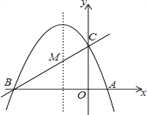
【题目】已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
【答案】(1). a=-1 ![]() (2). P1(
(2). P1(![]() ,
,![]() ),P2(-
),P2(-![]() ,-
,-![]() ).
).
【解析】试题分析:(1)由于抛物线的图象经过点(-1,0),那么此点坐标必满足抛物线的解析式,将其代入抛物线的解析式中,即可求得a的值,进而可得到抛物线的顶点坐标.
(2)将点P(t,t)代入抛物线的解析式中,即可求得符合条件的不动点的坐标.
试题解析:
(1)把点(-1,0)的坐标代入y=ax2+x+2中,得a=-1.
∴此抛物线的函数表达式为y=-x2+x+2=-![]()
![]() +
+![]() ,其顶点坐标是
,其顶点坐标是![]() .
.
(2)把点P(t,t)的坐标代入y=-x2+x+2中,
得t=-t2+t+2,解得t1=![]() ,t2=-
,t2=-![]() .
.
∴此抛物线上的不动点有两个,即点P1(![]() ,
,![]() ),P2(-
),P2(-![]() ,-
,-![]() ).
).

练习册系列答案
相关题目
【题目】(1)填表:
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你发现了什么规律?请用语言叙述这个规律:_______________________;
(3)根据你发现的规律填空:
①已知![]() =1.442,则
=1.442,则![]() =________,
=________, ![]() =__________;
=__________;
②已知![]() =0.076 97,则
=0.076 97,则![]() =__________.
=__________.