题目内容
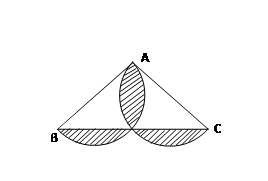
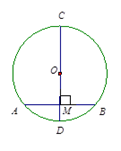
如图,在△ABC中,AB = AC,AB = 8,BC = 12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
A、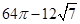 B、
B、
C、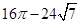 D、
D、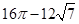

A、
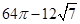 B、
B、
C、
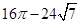 D、
D、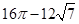
D
设半圆与底边的交点是D,连接AD.根据直径所对的圆周角是直角,得到AD⊥BC,再根据等腰三角形的三线合一,得到BD=CD=6,根据勾股定理即可求得AD的长,则阴影部分的面积是以AB为直径的圆的面积减去三角形ABC的面积.
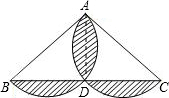
解:设半圆与底边的交点是D,连接AD.
∵AB是直径,
∴AD⊥BC.
又∵AB=AC,
∴BD=CD=6.
根据勾股定理,得
AD= =2
=2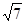 .
.
∵阴影部分的面积的一半=以AB为直径的半圆的面积-三角形ABD的面积
=以AC为直径的半圆的面积-三角形ACD的面积,
∴阴影部分的面积=以AB为直径的圆的面积-三角形ABC的面积=16π-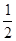 ×12×2
×12×2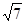
=16π-12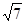 .
.
故选D.
此题综合运用了圆周角定理的推论、等腰三角形的三线合一、勾股定理、圆面积公式和三角形的面积公式.

解:设半圆与底边的交点是D,连接AD.
∵AB是直径,
∴AD⊥BC.
又∵AB=AC,
∴BD=CD=6.
根据勾股定理,得
AD=
 =2
=2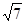 .
.∵阴影部分的面积的一半=以AB为直径的半圆的面积-三角形ABD的面积
=以AC为直径的半圆的面积-三角形ACD的面积,
∴阴影部分的面积=以AB为直径的圆的面积-三角形ABC的面积=16π-
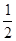 ×12×2
×12×2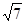
=16π-12
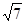 .
.故选D.
此题综合运用了圆周角定理的推论、等腰三角形的三线合一、勾股定理、圆面积公式和三角形的面积公式.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目

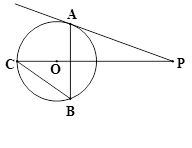
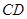 -线段DO的路线作匀速运动.设运动时间为
-线段DO的路线作匀速运动.设运动时间为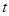 秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是
秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是 
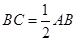 ,过点C作⊙O的切线,切点为D,则CD= ★ cm.
,过点C作⊙O的切线,切点为D,则CD= ★ cm.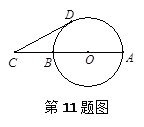
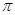 ?
?