题目内容
如图,已知⊙O的半径为2cm,点C是直径AB的延长线上一点,且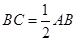 ,过点C作⊙O的切线,切点为D,则CD= ★ cm.
,过点C作⊙O的切线,切点为D,则CD= ★ cm.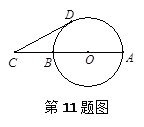
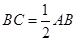 ,过点C作⊙O的切线,切点为D,则CD= ★ cm.
,过点C作⊙O的切线,切点为D,则CD= ★ cm.
连接OD,根据切线的性质得到∠CDO=90°,根据BC=1/2AB,推出OD=BC=OB=2,根据勾股定理即可求出答案.
解答: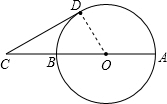 解:连接OD,
解:连接OD,
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠CDO=90°,
∵BC=/2AB,
∴OD=BC=OB=2,
由勾股定理得:CD= =
=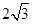 ,
,
故答案为: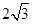 .
.
解答:
 解:连接OD,
解:连接OD,∵CD是⊙O的切线,
∴OD⊥CD,
∴∠CDO=90°,
∵BC=/2AB,
∴OD=BC=OB=2,
由勾股定理得:CD=
 =
=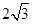 ,
,故答案为:
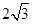 .
.
练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
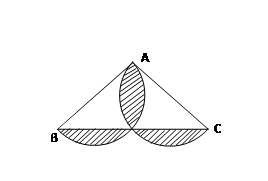
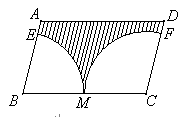
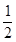 ∠AOC ,AD⊥CD于点D.
∠AOC ,AD⊥CD于点D.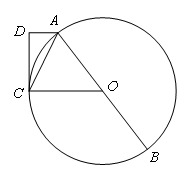
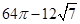 B、
B、
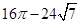 D、
D、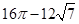
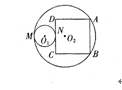
 OB.
OB.
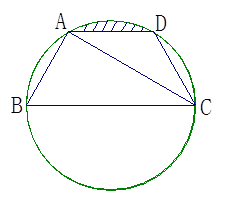
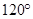 ,四边形ABCD周长为10.
,四边形ABCD周长为10.