��Ŀ����
����Ŀ���ڴ�����ȫ���������С��͡�ʡ�����������������У��������ˮ�����������ȹ���A��B������ˮ�����豸��20̨���Գ����ܱ���ˮ���д�������֪ÿ̨A���豸�۸�Ϊ12��Ԫ��ÿ̨B���豸�۸�Ϊ10��Ԫ��1̨A���豸��2̨B���豸ÿ�ܿ��Դ�����ˮ640�֣�2̨A���豸��3̨B���豸ÿ�ܿ��Դ�����ˮ1080�֣�
��1����A��B������ˮ�����豸ÿ�ֱܷ���Դ�����ˮ���ٶ֣�
��2��Ҫ��ʹ��ˮ�����������豸���ʽ���230��Ԫ����ÿ�ܴ�����ˮ�����ֲ�����4500�֣������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ��٣�
���𰸡���1��A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200�֣���2�����巽��������������A����ˮ�����豸13̨��B����ˮ�����豸7̨ʱ�����蹺���ʽ����٣�������226��Ԫ��
�������������������1������1̨A����ˮ�����豸��2̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ640�֣�2̨A����ˮ�����豸��3̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ1080�֣������г���Ӧ�Ķ�Ԫһ�η����飬�Ӷ�����⣻
��2��������������г���Ӧ�IJ���ʽ�飬�Ӷ����Եõ��������Ӷ��������ÿ�ַ��������ʽ𣬴Ӷ����Խ���⣮
�����������1����A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮx�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮy�֣���������
![]() ��
��
���![]() ��
��
��A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200�֣�
��2���蹺��A����ˮ�����豸x̨������B����ˮ�����豸��20��x��̨��
��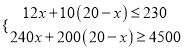 ��
��
���12.5��x��15��
��һ�ַ�������x=13ʱ��20��x=7�����ѵķ���Ϊ��13��12+7��10=226��Ԫ��
�ڶ��ַ�������x=14ʱ��20��x=6�����ѵķ���Ϊ��14��12+6��10=228��Ԫ��
�����ַ�������x=15ʱ��20��x=5�����ѵķ���Ϊ��15��12+5��10=230��Ԫ��
������A����ˮ�����豸13̨������B����ˮ�����豸7̨ʱ�����蹺���ʽ����٣�������226��Ԫ��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�