题目内容
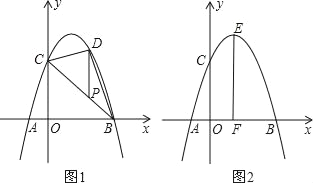
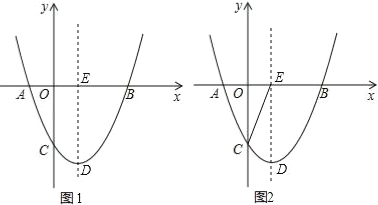
【题目】如图1,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣2),顶点为D,对称轴交x轴于点E.
(1)求该二次函数的解析式;
(2)设M为该抛物线对称轴左侧上的一点,过点M作直线MN∥x轴,交该抛物线于另一点N.是否存在点M,使四边形DMEN是菱形?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)连接CE(如图2),设点P是位于对称轴右侧该抛物线上一点,过点P作PQ⊥x轴,垂足为Q.连接PE,请求出当△PQE与△COE相似时点P的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)点M坐标为(1﹣
x﹣2;(2)点M坐标为(1﹣![]() ,﹣
,﹣![]() );(3)点P的坐标为(5,8)或(2,﹣2)或(
);(3)点P的坐标为(5,8)或(2,﹣2)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由A、B两点的坐标,利用待定系数法可求得二次函数的表达式;
(2)先求出顶点D(1,﹣![]() ),则DE=
),则DE=![]() ,根据四边形DMEN是菱形,点M的纵坐标为﹣
,根据四边形DMEN是菱形,点M的纵坐标为﹣![]() ,令
,令![]() x2﹣
x2﹣![]() x﹣2=﹣
x﹣2=﹣![]() ,解方程,即可求出点M坐标.
,解方程,即可求出点M坐标.
(3)分△COE∽△PQE和△COE∽△EQP两种情况进行讨论.
解:(1)设抛物线解析式为y=a(x+1)(x﹣3),
将点C(0,﹣2)代入,得:﹣3a=﹣2,
解得a=![]() ,
,
则抛物线解析式为![]()
(2)∵y=![]() x2﹣
x2﹣![]() x﹣2=
x﹣2=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ,
,
∴顶点D(1,﹣![]() ),即DE=
),即DE=![]() ,
,
∵四边形DMEN是菱形,
∴点M的纵坐标为﹣![]() ,
,
则![]() x2﹣
x2﹣![]() x﹣2=﹣
x﹣2=﹣![]() ,
,
解得x=1±![]() ,
,
∵M为该抛物线对称轴左侧上的一点,
∴x<1,
则x=1﹣![]() ,
,
∴点M坐标为(1﹣![]() ,﹣
,﹣![]() );
);
(3)∵C(0,﹣2),E(1,0),
∴OC=2,OE=1,
如图,设P(m,![]() m2﹣
m2﹣![]() m﹣2)(m>1),
m﹣2)(m>1),
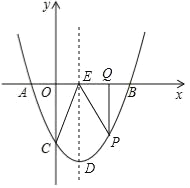
则PQ=|![]() m2﹣
m2﹣![]() m﹣2|,EQ=m﹣1,
m﹣2|,EQ=m﹣1,
①若△COE∽△PQE,则![]() 即
即![]()
解得m=0(舍)或m=5或m=2或m=﹣3(舍),
此时点P坐标为(5,8)或(2,﹣2);
②若△COE∽△EQP,则![]() 即
即![]()
解得m=![]() (负值舍去)或m=
(负值舍去)或m=![]() ,
,
此时点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
综上,点P的坐标为(5,8)或(2,﹣2)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】为了弘扬我国古代数学发展的伟大成就,某校九年级进行了一次数学知识竞赛,并设立了以我国古代数学家名字命名的四个奖项:“祖冲之奖”、“刘徽奖”、“赵爽奖”和“杨辉奖”,根据获奖情况绘制成如图1和图2所示的条形统计图和扇形统计图,并得到了获“祖冲之奖”的学生成绩统计表:
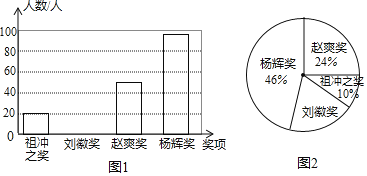
“祖冲之奖”的学生成绩统计表:
分数 | 80 | 85 | 90 | 95 |
人数 | 4 | 2 | 10 | 4 |
根据图表中的信息,解答下列问题:
![]() 这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
![]() 获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
![]() 在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“
在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“![]() ”,“
”,“![]() ”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点
”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点![]() 用列表法或树状图法求这个点在第二象限的概率.
用列表法或树状图法求这个点在第二象限的概率.