题目内容
【题目】把分别标有数字2,3,4,5的四个小球放入A袋,把分别标有数字 ![]() ,
, ![]() ,
, ![]() 的三个小球放入B袋,所有小球的形状、大小、质地均相同,A、B两个袋子不透明.
的三个小球放入B袋,所有小球的形状、大小、质地均相同,A、B两个袋子不透明.
(1)如果从A袋中摸出的小球上的数字为3,再从B袋中摸出一个小球,两个小球上的数字互为倒数的概率是;
(2)小明分别从A,B两个袋子中各摸出一个小球,请用树状图或列表法列出所有可能出现的结果,并求这两个小球上的数字互为倒数的概率.
【答案】
(1)![]()
(2)
解:树状图:
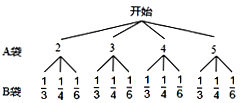
∵共有12种等可能的结果,这两个小球上的数字互为倒数的只有2种情况,
∴这两个小球上的数字互为倒数的概率为: ![]() =
= ![]() .
.
【解析】解:(1)∵从A袋中摸出的小球上的数字为3,
∴从B袋中摸出一个小球,两个小球上的数字互为倒数的只有 ![]() ,
,
∴从B袋中摸出一个小球,两个小球上的数字互为倒数的概率为 ![]() .
.
所以答案是: ![]() .
.
(1)由从B袋中摸出一个小球,两个小球上的数字互为倒数的只有 ![]() ,直接利用概率公式求解即可求得答案;
,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果为12,这两个小球上的数字互为倒数的情况为2,再利用概率公式即可求得答案.
【考点精析】利用列表法与树状图法和概率公式对题目进行判断即可得到答案,需要熟知当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目